上海理)如图,已知曲线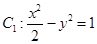 ,曲线
,曲线 ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与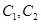 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.
(1)在正确证明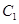 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线 与
与 有公共点,求证
有公共点,求证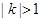 ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;
(3)求证:圆 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”.
(本小题满分12分)已知数列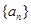 满足
满足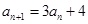 ,
,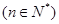 且
且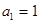 ,
,
(Ⅰ)求证:数列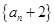 是等比数列;
是等比数列;
(Ⅱ)求数列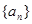 的前n项和
的前n项和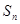 .
.
(本题14分)设各项均为正数的数列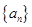 的前
的前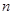 项和为
项和为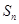 ,满足
,满足 且
且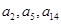 构成等比数列.
构成等比数列.
(1)证明: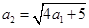 ;
;
(2)求数列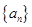 的通项公式;
的通项公式;
(3)证明:对一切正整数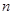 ,有
,有 ;
;
(本题13分) 数列 满足:
满足:
(1)证明:数列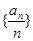 是等差数列;
是等差数列;
(2)设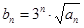 ,求数列
,求数列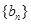 的前n项和
的前n项和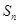 .
.
(本题12分)如图,A、B、C、D都在同一个与水平面垂直的平面内,B、D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°、30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1km.试探究图中B、D间距离与另外哪两点间距离相等,然后求B、D的距离(计算结果精确到0.01km,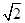 ≈1.414,
≈1.414,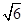 ≈2.449).
≈2.449).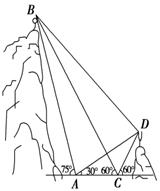
(本题12分)设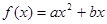 ,且
,且 ,
, .
.
求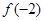 的取值范围即可。
的取值范围即可。