一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n。如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验。
假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为,且各件产品是否为优质品相互独立
(1)求这批产品通过检验的概率;
(2)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望。
如图,圆O1与圆O2内切于点A,其半径分别为r1与r2(r1>r2),圆O1的弦AB交圆O2于点C(O1不在AB上).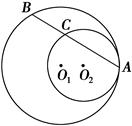
求证:AB∶AC为定值.
如图,在直三棱柱ABC A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.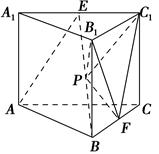
(1)证明:平面AEB⊥平面BB1C1C;
(2)证明:C1F∥平面ABE;
(3)设P是BE的中点,求三棱锥P B1C1F的体积.
如图,在四棱锥O ABCD中,底面ABCD为菱形,OA⊥平面ABCD,E为OA的中点,F为BC的中点,求证:(1)平面BDO⊥平面ACO;(2)EF∥平面OCD.
如图,四边形ABCD是矩形,平面ABCD⊥平面BCE,BE⊥EC.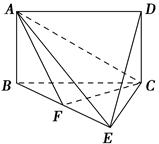
(1)求证:平面AEC⊥平面ABE;
(2)点F在BE上.若DE∥平面ACF,求 的值.
的值.
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,CD∥AP,AD与BC相交于点E,F为CE上一点,且DE2=EF·EC.
(1)求证:∠P=∠EDF;
(2)求证:CE·EB=EF·EP;
(3)若CE∶BE=3∶2,DE=6,EF=4,求PA的长.