某高校在2012年自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组：第1组[75，80)，第2组[80，85)，第3组[85，90)，第4组[90，95)，第5组[95，100]得到的频率分布直方图如图所示．
(1)分别求第3，4，5组的频率；
(2)若该校决定在笔试成绩较高的第3，4，5组中用分层抽样抽取6名学生进入第二轮面试，
(ⅰ)已知学生甲和学生乙的成绩均在第三组，求学生甲和学生乙恰有一人进入第二轮面试的概率；
(ⅱ)学校决定在这已抽取到的6名学生中随机抽取2名学生接受考官L的面试，设第4组中有
名学生被考官L面试，求的分布列和数学期望．
某一中学生心理咨询中心服务电话接通率为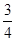
，某班3名同学商定明天分别就同一问题询问该服务中心，且每人只拨打一次，求他们中成功咨询的人数为X的分布列．
在一次口试中，要从10道题中随机抽出3道题进行回答，答对了其中2道题就获得及格，某考生会回答10道题中的6道题，那么他（她）获得及格的概率是多少？
一个袋子里有4个不同的红球，6个不同的白球，从中任取4个使得取出的球中红球比白球多的取法有多少种？红球不少于白球的取法又有多少种？
（1）把5本不同的书分给3名同学，每人一本，有多少种不同的分法？
（2）把5本相同的书分给3名同学，每人一本，有多少种不同的分法？
（选修4-5；不等式选讲）若
与不等式
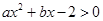同解，
的解集为空集，求
的取值范围．