随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是: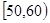 ,2;
,2;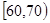 ,7;
,7;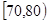 ,10;
,10;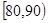 ,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.
,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.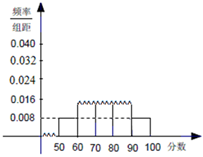
(1)求样本的人数及x的值;
(2)估计样本的众数,并计算频率分布直方图中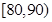 的矩形的高;
的矩形的高;
(3)从成绩不低于80分的样本中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为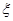 ,求
,求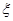 的数学期望.
的数学期望.
某旅游商品生产企业,2007年某商品生产的投入成本为1元/件,出厂价为1.2元/件,年销售量为10000件,因2008年调整黄金周的影响,此企业为适应市场需求,计划提高产品档次,适度增加投入成本。若每件投入成本增加的比例为 (
( ),则出厂价相应提高的比例为
),则出厂价相应提高的比例为 ,同时预计年销售量增加的比例为
,同时预计年销售量增加的比例为 。已知年利润
。已知年利润 (出厂价
(出厂价 投入成本)
投入成本) 年销售量。
年销售量。
(1)写出2008年预计的年利润 与投入成本增加的比例
与投入成本增加的比例 的关系式;
的关系式;
(2)为使2008年的年利润达到最大,则每件投入成本增加的比例 应是多少?此时最大年利润是多少?
应是多少?此时最大年利润是多少?
已知函数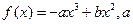 、
、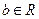 。
。
(1)讨论函数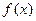 的奇偶性(只写结论,不要求证明);
的奇偶性(只写结论,不要求证明);
(2)在构成函数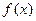 的映射
的映射 中,当输入值为
中,当输入值为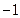 和2时分别对应的输出值为
和2时分别对应的输出值为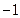 和
和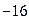 ,求
,求 、
、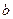 的值;
的值;
(3)在(2)的条件下,求函数 (
(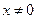 )的最大值。
)的最大值。
已知函数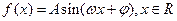 (其中
(其中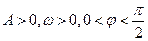 )的图象与
)的图象与 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为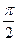 ,且图象上一个最低点为
,且图象上一个最低点为 。
。
(1)求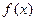 的解析式;
的解析式;
(2)当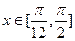 ,求
,求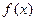 的值域。
的值域。
证明平行四边形四条边的平方和等于两条对角线的平方和.
已知点A(-1,2),B(2,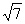 ),在x轴上求一点P,使|PA|=|PB|,并求|PA|的值.
),在x轴上求一点P,使|PA|=|PB|,并求|PA|的值.