设袋子中装有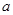 个红球,
个红球,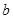 个黄球,
个黄球,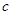 个蓝球,且规定:取出一个红球得1分,
个蓝球,且规定:取出一个红球得1分,
取出一个黄球2分,取出蓝球得3分。
(1)当 时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量
时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量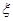 为取出此2球所得分数之和,.求
为取出此2球所得分数之和,.求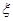 分布列;
分布列;
(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量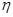 为取出此球所得分数.若
为取出此球所得分数.若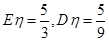 ,求
,求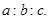
在 中,角
中,角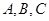 所对应的边分别为
所对应的边分别为 ,且
,且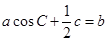
 ,
,
(1)求角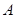 的大小
的大小
(2)若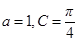 , 求
, 求 的面积
的面积
如图,圆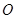 的直径
的直径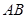 的延长线与弦
的延长线与弦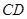 的延长线相交于点
的延长线相交于点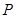 ,
,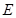 为圆
为圆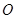 上一点,
上一点,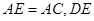 交
交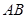 于点
于点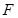 ,且
,且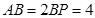
(1)求线段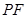 的长度
的长度
(2)若圆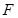 与圆
与圆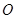 内切,直线
内切,直线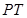 与圆
与圆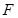 切于点
切于点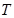 ,
,
求线段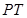 的长度
的长度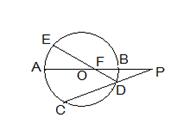
(本小题满分12分)如图,在正方体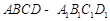 中,
中,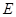 、
、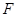 分别为棱
分别为棱 、
、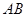 的中点.
的中点.
(1)求证:平面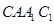 ⊥平面
⊥平面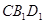 ;
;
(2)如果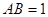 ,一个动点从点
,一个动点从点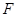 出发在正方体的表面上依次经过棱
出发在正方体的表面上依次经过棱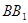 、
、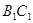 、
、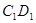 、
、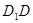 、
、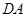 上的点,最终又回到点
上的点,最终又回到点 ,指出整个路线长度的最小值并说明理由.
,指出整个路线长度的最小值并说明理由.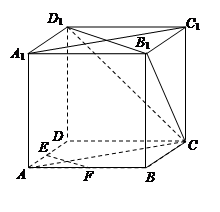
(本小题12分)如图,四棱锥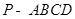 中,底面
中,底面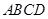 是正方形,
是正方形,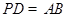 ,
, 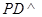 底面
底面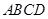 ,
,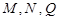 分别在
分别在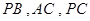 上,且
上,且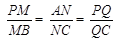
(1)求证:平面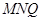 ∥平面
∥平面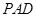 .
.
(2)求直线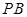 与平面面
与平面面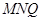 所成角的正弦值.
所成角的正弦值.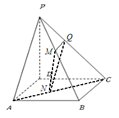
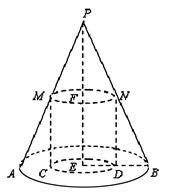
(本小题12分)如图,在底面半径为3,母线长为5的圆锥中内接一个高为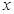 的圆柱.
的圆柱.
(1)求圆锥的体积.
(2)当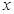 为何值时,圆柱的表面积最大,并求出最大值.
为何值时,圆柱的表面积最大,并求出最大值.