已知曲线C的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: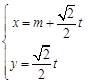 (
( 是参数).
是参数).
(1)将曲线C的极坐标方程化为直角坐标方程,将直线 的参数方程化为普通方程;
的参数方程化为普通方程;
(2)若直线l与曲线C相交于A、B两点,且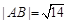 ,试求实数m值.
,试求实数m值.
(本题13分)已知抛物线的焦点 在
在 轴上,抛物线上一点
轴上,抛物线上一点 到准线的距离是
到准线的距离是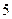 ,过点
,过点 的直线与抛物线交于
的直线与抛物线交于 ,
,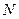 两点,过
两点,过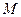 ,
,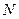 两点分别作抛物线的切线,这两条切线的交点为
两点分别作抛物线的切线,这两条切线的交点为 .
.
(1)求抛物线的标准方程;
(2)求 的值;
的值;
(3)求证: 是
是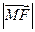 和
和 的等比中项.
的等比中项.
(本小题满分12分)如图,多面体ABCDS中,面ABCD为矩形,
 ,
,
(1)求证:CD ;
;
(2)求AD与SB所成角的余弦值;
(3)求二面角A—SB—D的余弦值.
(本小题满分12分)
四枚不同的金属纪念币 、
、 、
、 、
、 ,投掷时,A、B两枚正面向上的概率为分别为
,投掷时,A、B两枚正面向上的概率为分别为 ,另两枚C、D正面向上的概率分别为
,另两枚C、D正面向上的概率分别为
 .这四枚纪念币同时投掷一次,设
.这四枚纪念币同时投掷一次,设 表示出现正面向上的枚数。
表示出现正面向上的枚数。
(1)若A、B出现一正一反与C、D出现两正的概率相等,求 的值;
的值;
(2)求 的分布列及数学期望(用
的分布列及数学期望(用 表示);
表示);
(3)若有2枚纪念币出现正面向上的概率最大,求 的取值范围。
的取值范围。
(本小题满分12分)在 中,已知内角
中,已知内角 所对的边分别为
所对的边分别为 ,向量
,向量
 ,且
,且 //
// ,
, 为锐角.
为锐角.
(1)求角 的大小;
的大小;
(2)设 ,求
,求 的面积
的面积 的最大值.
的最大值.
(本小题满分12分)
已知椭圆C的中心在原点、焦点在 轴上,椭圆C上的点到焦点的最大值为3,最小值为1.
轴上,椭圆C上的点到焦点的最大值为3,最小值为1.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线 :
: 与
与 椭圆交于不同的两点M,N(M,N不是左、右顶点),且以MN为直径的圆经过椭圆的右顶点A.求证:直线
椭圆交于不同的两点M,N(M,N不是左、右顶点),且以MN为直径的圆经过椭圆的右顶点A.求证:直线 过定点,并求出定点的坐标.
过定点,并求出定点的坐标.