已知曲线C的极坐标方程为 ,直线
,直线 的参数方程为
的参数方程为 (t为参数,
(t为参数, )
)
(1)把曲线C的极坐标方程化为直角坐标方程,并说明曲线C的形状;
(2)若直线 经过点
经过点 ,求直线
,求直线 被曲线C截得的线段AB的长。
被曲线C截得的线段AB的长。
从社会效益和经济利益出发,某地投入资金进行生态环境建设,并以此发展旅游产业,根据规划,本年度投入800万元,以后每年投入将比上年减少 。本年度当地旅游收入估计为400万元,预计今后的旅游业收入每年比上一年增加
。本年度当地旅游收入估计为400万元,预计今后的旅游业收入每年比上一年增加
(1)设 年内(本年度为第一年)总投入为
年内(本年度为第一年)总投入为 万元,旅游业总收入为
万元,旅游业总收入为 万元,写出
万元,写出 ,
, 的表达式;
的表达式;
(2)至少经过几年,旅游业的总收入才能超过投入?
已知等差数列 的公差为2,其前n项和
的公差为2,其前n项和
(I)求p的值及
(II)若 ,记数列
,记数列 的前n项和为
的前n项和为 ,求使
,求使 成立的最小正整数n的值。
成立的最小正整数n的值。
已知: 为常数)
为常数)
(1)若 ,求
,求 的最小正周期及单调区间;
的最小正周期及单调区间;
(2)若 在[
在[ 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求 的值.
的值.
已知向量 ,且
,且 。
。
求 及
及 。
。
如图,甲船以每小时 海里的速度向正北方航行,乙船按固定方向匀速直线航行。当甲船位于处
海里的速度向正北方航行,乙船按固定方向匀速直线航行。当甲船位于处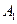 时,乙船位于甲船的北偏西
时,乙船位于甲船的北偏西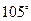 方向的
方向的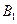 处,此时两船相距20海里,当甲船航行20分钟到达
处,此时两船相距20海里,当甲船航行20分钟到达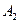 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西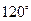 方向的
方向的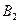 处,此时两船相距
处,此时两船相距 海里。问:乙船每小时航行多少海里?
海里。问:乙船每小时航行多少海里?