演讲答辩由7位评委老师打分，民主测评由50名学生代表一人一票，按“优秀、良好、一般”三选一投票．如图是7位评委对小明“演讲答辩”的评分统计图及50位同学民主测评票数统计图．
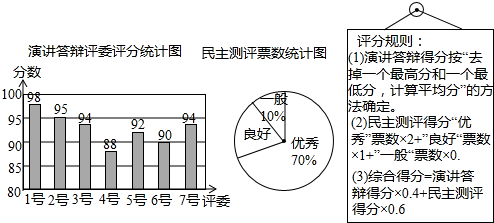
（1）求小明演讲答辩所得分数的众数，以及民主测评为“良好”票数的扇形圆心角度数；
（2）求小明的综合得分是多少？
（3）在竞选中，小亮的民主测评得分为82分，如果他的综合得分不小于小明的综合得分，他的演讲答辩得分至少要多少分？
某商场用36000元购进甲、乙两种商品，销售完后共获利6000元．其中甲种商品每件进价120元，售价138元；乙种商品每件进价100元，售价120元．
（1）、该商场购进甲、乙两种商品各多少件？
（2）、商场第二次以原进价购进甲、乙两种商品，购进乙种商品的件数不变，而购进甲种商品的件数是第一次的2倍，甲种商品按原售价出售，而乙种商品打折销售．若两种商品销售完毕，要使第二次经营活动获利不少于8160元，乙种商品最低售价为每件多少元？
如图，AD为△ABC的中线，BE为△ABD的中线．
（1）、猜想：△ABD与△ADC的面积有何关系？并简要说明理由；
（2）、在△BED中作ED边上的高；
（3）、若△ABC的面积为40，BD=5，则△BDE中BD边上的高为多少？
如图，在△ABC中，∠B=60°，∠C=20°，AD为△ABC的高，AE为角平分线．求∠EAD的度数．
如图，在一块边长为acm的正方形纸板四角，各剪去一个边长为bcm（b＜
）的正方形，利用因式分解计算当a=13.2，b=3.4时，剩余部分的面积．
（1）先化简，再求值：（x+3）（x﹣3）﹣x（x﹣2），其中x=4．
（2）解不等式组
，并把解集在数轴上表示出来．