如图,在平面直角坐标系xOy中,椭圆 的离心率为
的离心率为 ,过椭圆右焦点
,过椭圆右焦点 作两条互相垂直的弦
作两条互相垂直的弦 与
与 .当直线
.当直线 斜率为0时,
斜率为0时, .
.
(1)求椭圆的方程;
(2)求 的取值范围.
的取值范围.
已知抛物线 与直线
与直线 相切于点
相切于点 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若对任意 ,不等式
,不等式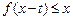 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
记函数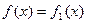 ,
,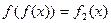 ,它们定义域的交集为
,它们定义域的交集为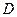 ,若对任意的
,若对任意的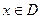 ,
,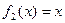 ,则称
,则称 是集合
是集合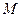 的元素.
的元素.
(1)判断函数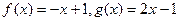 是否是
是否是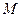 的元素;
的元素;
(2)设函数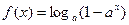 ,求
,求 的反函数
的反函数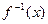 ,并判断
,并判断 是否是
是否是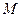 的元素;
的元素;
(Ⅰ)已知函数: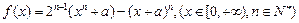 求函数
求函数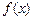 的最小值;
的最小值;
(Ⅱ)证明: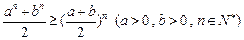 ;
;
(Ⅲ)定理:若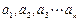 均为正数,则有
均为正数,则有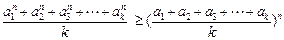 成立(其中
成立(其中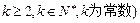 .请你构造一个函数
.请你构造一个函数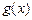 ,证明:
,证明:
当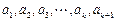 均为正数时,
均为正数时,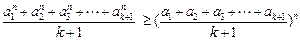 .
.
已知动圆Q经过点A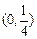 ,且与直线
,且与直线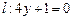 相切,动圆圆心Q的轨迹为曲线C,过定点
相切,动圆圆心Q的轨迹为曲线C,过定点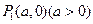 作与y轴平行的直线且和曲线C相交于点M1,然后过点M1作C的切线和x轴交于点
作与y轴平行的直线且和曲线C相交于点M1,然后过点M1作C的切线和x轴交于点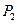 ,再过
,再过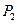 作与y轴平行的直线且和C相交于点M2,又过点M2作C的切线和x轴交于点
作与y轴平行的直线且和C相交于点M2,又过点M2作C的切线和x轴交于点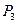 ,如此继续下去直至无穷,记△
,如此继续下去直至无穷,记△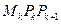 的面积为
的面积为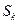
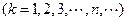

(Ⅰ)求曲线C的方程;
(Ⅱ)试求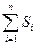 的值。
的值。
设
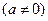 ,令
,令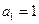 ,
,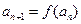 ,又
,又 ,
, .
.
(Ⅰ)判断数列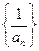 是等差数列还是等比数列并证明;
是等差数列还是等比数列并证明;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)求数列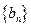 的前
的前 项和.
项和.