如图,已知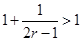 ,
, ,
, ,
,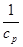 分别是椭圆
分别是椭圆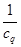 的四个顶点,△
的四个顶点,△ 是一个边长为2的等边三角形,其外接圆为圆
是一个边长为2的等边三角形,其外接圆为圆 .
.
(1)求椭圆 及圆
及圆 的方程;
的方程;
(2)若点 是圆
是圆 劣弧
劣弧 上一动点(点
上一动点(点 异于端点
异于端点 ,
, ),直线
),直线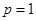 分别交线段
分别交线段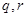 ,椭圆
,椭圆 于点
于点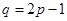 ,
,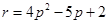 ,直线
,直线 与
与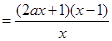 交于点
交于点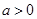 .
.
(ⅰ)求 的最大值;
的最大值;
(ⅱ)试问: ,
,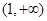 两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.
两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.
已知等差数列 的公差大于0,且
的公差大于0,且 是方程
是方程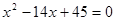 的两根。数列
的两根。数列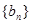 的前n项和为
的前n项和为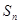 ,且
,且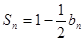 。
。
(1)求通项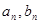 ;
;
(2)记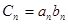 ,求证:
,求证: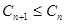 。
。
已知 :不等式
:不等式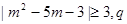 :函数
:函数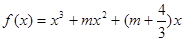 +6在
+6在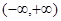 上有极值,求使“p且q”为真命题时m的范围。
上有极值,求使“p且q”为真命题时m的范围。
设函数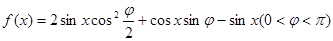 在
在 处取得最小值,
处取得最小值,
(1)求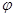 的值;
的值;
(2)在△ABC中,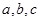 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知 ,求角C。
,求角C。
(本小题满分12分) 过椭圆 的左顶点A做斜率为2的直线,与椭圆的另一个交点为B,与y轴的交点为C,已知
的左顶点A做斜率为2的直线,与椭圆的另一个交点为B,与y轴的交点为C,已知 .
.
(Ⅰ)求椭圆的离心率;
(Ⅱ)设动直线y=kx+m与椭圆有且只有一个公共点P,且与直线x=4相交于点Q,若x轴上存在一定点
M(1,0),使得PM⊥QM,求椭圆的方程.
(本小题满分共12分)已知函数 ,
,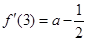
(1)若g(x)=f(x+1),求证:曲线g(x)上的任意一点处的切线与直线x=0和直线y=ax围成的三角形面积为定值;
(2)若f(3)=3,是否存在实数m,k,使得f(x)+f(m﹣x)=k对于定义域内的任意x都成立;