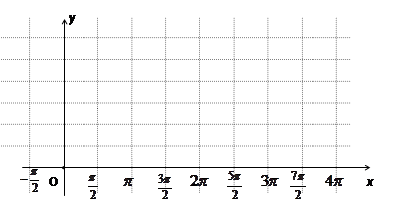某大型公益活动从一所名牌大学的四个学院中选出了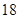 名学生作为志愿者,参加相关的活
名学生作为志愿者,参加相关的活
动事宜.学生来源人数如下表:
| 学院 |
外语学院 |
生命科学学院 |
化工学院 |
艺术学院 |
| 人数 |
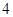 |
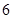 |
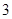 |
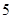 |
(1)若从这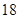 名学生中随机选出两名,求两名学生来自同一学院的概率;
名学生中随机选出两名,求两名学生来自同一学院的概率;
(2)现要从这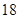 名学生中随机选出两名学生向观众宣讲此次公益活动的主题.设其中来自外语学院的人数为
名学生中随机选出两名学生向观众宣讲此次公益活动的主题.设其中来自外语学院的人数为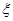 ,令
,令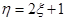 ,求随机变量
,求随机变量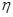 的分布列及数学期望
的分布列及数学期望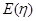 .
.
已知函数 .
.
(Ⅰ)若 ,求
,求 的取值范围;
的取值范围;
(Ⅱ)证明: .
.
已知函数f(x)=(1+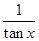 )sin2x+
)sin2x+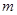 sin(x+
sin(x+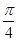 )sin(x-
)sin(x-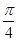 ).
).
(1)当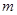 =0时,求f(x)在区间[
=0时,求f(x)在区间[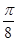 ,
,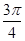 ]上的取值范围;
]上的取值范围;
(2)当tan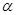 =2时,f(
=2时,f(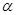 )=
)=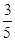 ,求
,求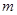 的值.
的值.
在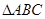 中,角
中,角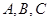 所对的边分别为
所对的边分别为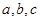 ,且满足
,且满足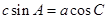 .
.
(I)求角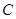 的大小;
的大小;
(II)求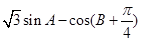 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角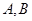 的大小.
的大小.
(Ⅰ)①证明两角和的余弦公式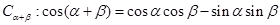 ;②由
;②由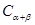 推导两角和的正弦公式
推导两角和的正弦公式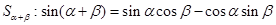
(Ⅱ)已知△ABC的面积 S=12,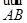 •
•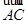 =3,且 cosB=
=3,且 cosB=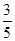 ,求cosC.
,求cosC.
(本小题12分)已知函数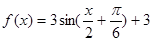
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出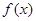 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;
(3)说明此函数图象可由 上的图象经怎样的变换得到.
上的图象经怎样的变换得到.