如图AE∥BD,∠CBD=57°,∠AEF=125°,求∠C的度数,并说明理由。
先化筒 ,然后从介于-4和4之间的整数中,选取一个你认为合适的x的值代入求值.
,然后从介于-4和4之间的整数中,选取一个你认为合适的x的值代入求值.
如图,直角坐标系中,以点A(1,0)为圆心画圆,点M(4,4)在⊙A上,直线y=-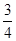 x+b过点M,分别交x轴、y轴于B、C两点.
x+b过点M,分别交x轴、y轴于B、C两点.求⊙A的半径和b的值;
判断直线BC与⊙A的位置关系,并说明理由;
若点P在⊙A上,点Q是y轴上C点下方的一点,当△PQM为等腰直角三角形时,请直接写出满足条件的点Q(0,k)(k为整数)坐标.

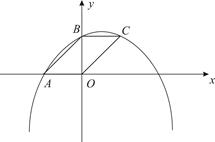
如图,已知抛物线y=-x2+bx+c与x轴负半轴交于点A,与y轴正半轴交于点B,且OA=OB.求b+c的值
若点C在抛物线上,且四边形OABC是平行四边形,试求抛物线的解析式;
在(2)的条件下,作∠OBC的角平分线,与抛物线交于点P,求点P的坐标.
问题背景:在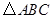 中,
中,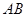 、
、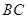 、
、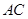 三边的长分别为
三边的长分别为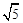 、
、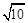 、
、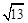 ,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点
,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点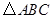 (即
(即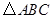 三个顶点都在小正方形的顶点处),如图①所示.这样不需求
三个顶点都在小正方形的顶点处),如图①所示.这样不需求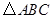 的高,而借用网格就能计算出它的面积.
的高,而借用网格就能计算出它的面积.请你将
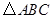 的面积直接填写在横线上._________________________思维拓展:
的面积直接填写在横线上._________________________思维拓展:我们把上述求
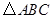 面积的方法叫做构图法.若
面积的方法叫做构图法.若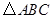 三边的长分别为
三边的长分别为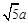 、
、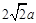 、
、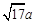 (
(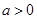 ),请利用图②的正方形网格(每个小正方形的边长为
),请利用图②的正方形网格(每个小正方形的边长为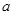 )画出相应的
)画出相应的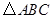 ,并求出它的面积.探索创新:
,并求出它的面积.探索创新:若
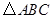 三边的长分别为
三边的长分别为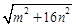 、
、 、
、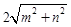 (
(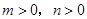 ,且
,且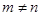 ),试运用构图法求出这三角形的面积.
),试运用构图法求出这三角形的面积.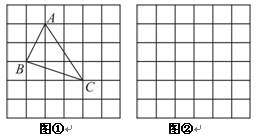
我县城区青印溪两岸堤坝的横截面是如图所示的梯形ABCD,背水坡AD的坡度i(即tanα)为1:1.2,坝高为5m,现为响应上级“搞好民生水利工程”的号召,决定加固堤坝。要求坝顶CD加宽lm,形成新的背水坡EF,其坡度为1:1.4,已知堤坝总长度为3000m完成该工程需要多少土方?
该工程由甲、乙两个工程队同时合作完成,按原计划需要20天.准备开工前接到上级通知,汛期可能提前,要求两个工程队提高工作效率,甲队工作效率提高30%,乙队工作效率提高40%,结果提前5天完成.问这两个工程队原计划每天各完成多少土方?
