在平面直角坐标系xOy中，已知抛物线yax2bxc与x轴交于-优题课

题文

在平面直角坐标系 $xOy$ 中，已知抛物线 $y = a x^{2} + bx + c$ 与 $x$ 轴交于 $A (- 1, 0)$ ， $B (4, 0)$ 两点，与 $y$ 轴交于点 $C (0, - 2)$ ．

（1）求抛物线的函数表达式；

（2）如图1，点 $D$ 为第四象限抛物线上一点，连接 $AD$ ， $BC$ 交于点 $E$ ，连接 $BD$ ，记 $ΔBDE$ 的面积为 $S_{1}$ ， $ΔABE$ 的面积为 $S_{2}$ ，求 $\frac{S_{1}}{S_{2}}$ 的最大值；

（3）如图2，连接 $AC$ ， $BC$ ，过点 $O$ 作直线 $l / / BC$ ，点 $P$ ， $Q$ 分别为直线 $l$ 和抛物线上的点．试探究：在第一象限是否存在这样的点 $P$ ， $Q$ ，使 $ΔPQB ∽ ΔCAB$ ．若存在，请求出所有符合条件的点 $P$ 的坐标；若不存在，请说明理由．

科目数学题型解答题难度较难

知识点：二次函数的性质待定系数法求二次函数解析式二次函数综合题

登录免费查看答案和解析

相关试题

如图，已知抛物线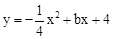与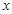轴相交于A、B两点，与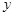轴相交于点C，若已知B点的坐标为B（8，0）.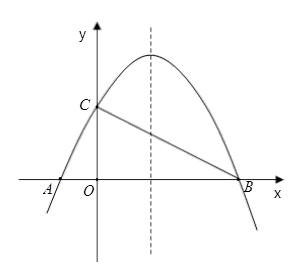

（1）求抛物线的解析式及其对称轴方程；
（2）连接AC、BC，试判断△AOC与△COB是否相似？并说明理由；
（3）M为抛物线上BC之间的一点，N为线段BC上的一点，若MN∥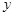轴，求MN的最大值；
（4）在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由.

如图E为正方形ABCD边BC延长线上一点，AE交DC于F，FG∥BE交DE于G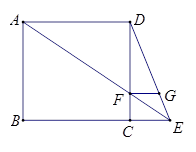

（1）求证：FG=FC；
（2）若FG=1,AD=3，求tan∠GFE的值.

通过锐角三角比的学习，我们已经知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长比与角的大小之间可以相互转化. 类似的我们可以在等腰三角形中建立边角之间的联系.我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）. 如下图在△ABC中，AB=AC,顶角A的正对记作sadA，这时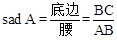. 我们容易知道一个角的大小与这个角的正对值也是互相唯一确定的.根据上述角的正对定义，解下列问题：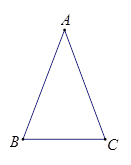

（1）sad60º=_____________；sad90º=________________。
（2）对于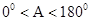，的正对值sadA的取值范围是_____________。
（3）试求sad36º的值.

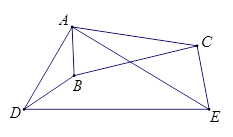
如图已知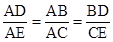：，求证：.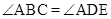

已知一个二次函数的顶点A的坐标为（1，0），且图像经过点B（2，3）.
（1）求这个二次函数的解析式.
（2）设图像与y轴的交点为C，记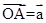，试用表示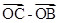（直接写出答案）

试卷网试题网古诗词网作文网范文网