已知数列 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且 是
是 和
和 的等比中项.
的等比中项.
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为 ,
, ,试问当
,试问当 为何值时,
为何值时, 最大?并求出
最大?并求出 的最大值.
的最大值.
已知 ,
, ,
, 分别是
分别是 的三个内角
的三个内角 ,
, ,
, 所对的边,且
所对的边,且 .
.
(1)求角 的值;
的值;
(2)若 ,
, 的面积
的面积 ,求
,求 的值.
的值.
已知函数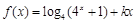
 是偶函数.
是偶函数.
(1)求实数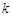 的值;
的值;
(2)设函数 ,若函数
,若函数 与
与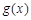 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数 的取值范围.
的取值范围.
如图是函数 的部分图象,直线
的部分图象,直线 是其两条对称轴.
是其两条对称轴.
(1)求函数 的解析式;
的解析式;
(2)写出函数 的单调增区间;
的单调增区间;
(3)若 ,且
,且 ,求
,求 的值.
的值.
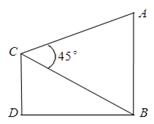
座落于我市红梅公园边的天宁宝塔堪称中华之最,也堪称佛塔世界之最.如图,已知天宁宝塔AB高度为150米,某大楼CD高度为90米,从大楼CD顶部C看天宁宝塔AB的张角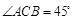 ,求天宁宝塔AB与大楼CD底部之间的距离BD.
,求天宁宝塔AB与大楼CD底部之间的距离BD.