(本小题满分12分)如图,已知三棱柱ABC-A'B'C'侧棱垂直于底面,AB="AC," ∠BAC=900,点M,N分别为A'B和B'C'的中点.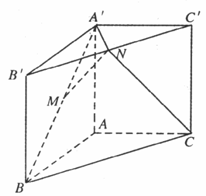
(Ⅰ)证明:MN//平面AA'C'C;
(Ⅱ)设AB= AA',当A为何值时,CN⊥平面A'MN,试证明你的结论.
AA',当A为何值时,CN⊥平面A'MN,试证明你的结论.
已知函数 ,
, .
.
(Ⅰ)求方程 =0的根;
=0的根;
(Ⅱ)求 的最大值和最小值.
的最大值和最小值.
已知函数


 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若函数 的图像在点
的图像在点 处的切线的斜率为
处的切线的斜率为 ,问:
,问:  在什么范围取值时,对于任意的
在什么范围取值时,对于任意的 ,函数
,函数 在区间
在区间 上总存在极值?
上总存在极值?
(Ⅲ)当 时,设函数
时,设函数 ,若在区间
,若在区间 上至少存在一个
上至少存在一个 ,使得
,使得 成立,试求实数
成立,试求实数 的取值范围.
的取值范围.
已知点 分别为椭圆
分别为椭圆 的左、右焦点,点
的左、右焦点,点 为椭圆上任意一点,
为椭圆上任意一点, 到焦点
到焦点 的距离的最大值为
的距离的最大值为 ,且
,且 的最大面积为
的最大面积为 .
.
(I)求椭圆 的方程。
的方程。
(II)点 的坐标为
的坐标为 ,过点
,过点 且斜率为
且斜率为 的直线
的直线 与椭圆
与椭圆 相交于
相交于 两点。对于任意的
两点。对于任意的 是否为定值?若是求出这个定值;若不是说明理由。
是否为定值?若是求出这个定值;若不是说明理由。
已知数列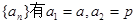 (常数p>0),对任意的正整数n,
(常数p>0),对任意的正整数n,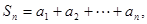 并有
并有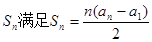
(I)试判断数列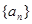 是否是等差数列,若是,求其通项公式,若不是,说明理由;
是否是等差数列,若是,求其通项公式,若不是,说明理由;
(II)令 的前n项和,求证:
的前n项和,求证: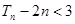
如图4,已知平面 是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线
是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线 的中点,已知
的中点,已知
(I))求证: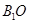 ⊥平面
⊥平面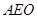 ;
;
(II)求二面角 的余弦值.
的余弦值.
(Ⅲ)求三棱锥 的体积.
的体积.