一袋中装有4个形状、大小完全相同的球,其中黑球2个,白球2个,假设每个小球从袋中被取出的可能性相同,首相由甲取出2个球,并不在将他们原袋中,然后由乙取出剩下的2个球.规定取出一个黑球记1分,取出一个白球记2分,取出球的总积分多者获胜.
(1)求甲、乙平局的概率;
(2)假设可以选择取球的先后顺序,应选择先取,还是后取,请说明理由.
设椭圆 ,直线
,直线 过椭圆左焦点
过椭圆左焦点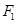 且不与
且不与 轴重合,
轴重合,  与椭圆交于
与椭圆交于 ,两点,当
,两点,当 与
与 轴垂直时,
轴垂直时, ,若点
,若点 且
且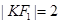
(1)求椭圆 的方程;
的方程;
(2)直线 绕着
绕着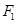 旋转,与圆
旋转,与圆 交于
交于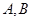 两点,若
两点,若 ,求
,求 的面积
的面积 的取值范围(
的取值范围( 为椭圆的右焦点)。
为椭圆的右焦点)。
如图在四棱锥 中,底面
中,底面 是菱形,
是菱形, ,
, 底面
底面 ,
, 是
是 的中点,
的中点,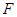 是
是 中点。
中点。
(1)求证: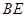 ∥平面
∥平面 ;
;
(2)求证:平面 ⊥平面
⊥平面 ;
;
(3)求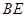 与平面
与平面 所成的角。
所成的角。
一个盒子中有5只同型号的灯泡,其中有3只合格品,2只不合格品。现在从中依次取出2只,设每只灯泡被取到的可能性都相同,请用“列举法”解答下列问题:
(1)求第一次取到不合格品,且第二次取到的是合格品的概率;
(2)求至少有一次取到不合格品的概率。
已知锐角△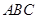 三个内角分别为
三个内角分别为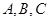 向量
向量 与向量
与向量 是共线向量.
是共线向量.
(1)求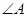 的值;
的值;
(2)求函数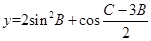 的值域.
的值域.
已知函数 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)求证:当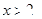 时,
时,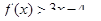 .
.