在水平光滑的绝缘如图所示的直角坐标系中，对于第I象限和第IV象限，其中一个象限有垂直纸面向外的匀强磁场B，另一象限有平行纸面的匀强电场E，一个比荷为
= 2×108 C/kg的电荷，从坐标原点处以速度v0=4×106 m/s进入第IV象限，v0与x轴成45°，已知电荷通过P(
，0)点第一次经x轴进入第I象限，并且经过时间t =2×10–4 s，以大小相同、方向相反的速度回到P(，0)点．
（1）问电荷带正电还是带负电，匀强电场存在哪个象限，方向如何?
（2）求磁感应强度和电场强度的大小；
（3）求电荷第三次经过x轴的位置．
（4）若电荷第三次经过x轴时突然改变匀强电场的大小，使电荷第四次回到x轴时恰好是P点，求改变后的电场强度大小
如图所示，物体在长4m的斜面顶端由静止下滑，然后进入由圆弧与斜面连接的水平面，(由斜面滑至平面时无能量损失)若物体与斜面及水平面的动摩擦因数均为0.5，斜面倾角为37°，取g=10m/s2，已知：sin37°＝0.6，cos37°＝0.8。求：
（1）物体到达斜面底端时的速度大小；
（2）物体能在水平面上滑行的距离。
人造地球同步卫星是一种特殊的人造卫星，简称同步卫星，一般多用于通讯，它相对地面静止，犹如悬挂在地球正上空一样。设地球的半径为R，自转的角速度为ω，地面附近的重力加速度为g。试求出同步卫星离地球表面的高度。
如图所示的平行板器件中，存在相互垂直的匀强磁场和匀强电场，磁场的磁感应强度B1 =" 0.40" T，方向垂直纸面向里，电场强度E = 2.0×105 V/m，PQ为板间中线．紧靠平行板右侧边缘xOy坐标系的第一象限内，有垂直纸面的正三角形匀强磁场区域，磁感应强度B2 =" 0.25" T。一束带电量q = 8.0×10-19 C，质量m = 8.0×10-26 kg的正离子从P点射入平行板间，不计重力，沿中线PQ做直线运动，穿出平行板后从y轴上坐标为（0，0.2m）的Q点垂直y轴射向三角形磁场区，离子通过x轴时的速度方向与x轴正方向夹角为60°。则：
（1）离子运动的速度为多大？
（2）试讨论正三角形区域内的匀强磁场方向垂直纸面向里和垂直纸面向外两种情况下，正三角形磁场区域的最小边长分别为多少？并分别求出其在磁场中运动的时间。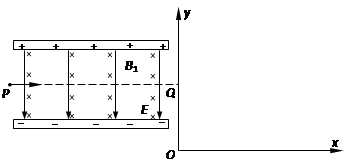
如图所示，质量为M=400g的铁板固定在一根轻弹簧上方，铁板的上表面保持水平．弹簧的下端固定在水平面上，系统处于静止状态．在铁板中心的正上方有一个质量为m=100g的木块，从离铁板上表面高h=80cm处自由下落．木块撞到铁板上以后不再离开，两者一起开始做简谐运动．木块撞到铁板上以后，共同下降了l1=2.0cm时刻，它们的共同速度第一次达到最大值．又继续下降了l2=8.0cm后，它们的共同速度第一次减小为零．空气阻力忽略不计，重力加速度取g=10m/s2．求：
（1）若弹簧的弹力跟弹簧的形变量成正比，比例系数叫做弹簧的劲度系数，用k表示．求本题中弹簧的劲度系数k；
（2）从木块和铁板共同开始向下运动到它们的共同速度第一次减小到零的过程中，弹簧的弹性势能增加了多少？
（3）在振动过程中，铁板对木块的弹力的最小值N是多少？
如图所示，光滑绝缘的正方形水平桌面边长为d =" 0.48" m，离地高度h =" 1.25" m。桌面上存在一水平向左的匀强电场(其余位置均无电场)，电场强度E = 1×104 N/C。在水平桌面上某一位置P处有一质量m =" 0.01" kg，电量q = 1×10-6 C的带正电小球以初速v0=1m/s向右运动。空气阻力忽略不计，重力加速度g ="10" m/s2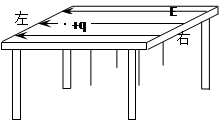
（1）求小球在桌面上运动时的加速度；
（2）P处距右端桌面多远时，小球从开始运动到最终落地的水平距离最大，并求出该最大水平距离。