已知椭圆 的中心在原点
的中心在原点 ,焦点在
,焦点在 轴上,离心率为
轴上,离心率为 ,右焦点到右顶点的距离为
,右焦点到右顶点的距离为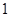 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)若直线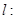
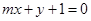 与椭圆
与椭圆 交于
交于 两点,是否存在实数
两点,是否存在实数 ,使
,使 成立?若存在,求
成立?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本题满分14分).如图,在棱长为4的正方体ABCD-A1B1C1D1中,E是D1C1上的一点且EC1=3D1 E,
(1) 求直线BE与平面ABCD所成角的正切值;
(2)求异面直线BE与CD所成角的余弦值. 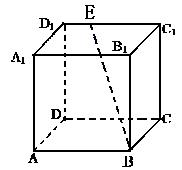
(本题满分12分).如图,在三棱柱ABC- 中,点E,D分别是
中,点E,D分别是 与BC的中点.
与BC的中点.
求证:平面 EB//平面AD
EB//平面AD .
.
(本题满分12分).画出右边水平放置的几何体的三视图.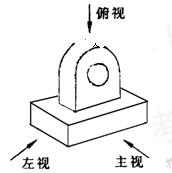
已知离心率为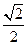 的椭圆
的椭圆 过点
过点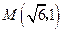 ,
, 是坐
是坐
标原点.
(1)求椭圆 的方程;
的方程;
(2)已知点 为椭圆
为椭圆 上相异两点,且
上相异两点,且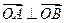 ,判定直线
,判定直线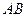 与圆
与圆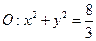 的
的
位置关系,并证明你的结论.
已知函数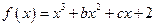 在
在 处取得极值
处取得极值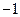 .
.
(1)求 的值;
的值;
(2)若关于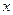 的方程
的方程 在区间
在区间 上有实根,求实数
上有实根,求实数 的取值范围.
的取值范围.