(本小题满分12分)如图,四棱锥P—ABCD中,底面ABCD为菱形,PD=AD,∠DAB="60°," PD⊥底面ABCD.
(1)求作平面PAD与平面PBC的交线,并加以证明;
(2)求PA与平面PBC所成角的正弦值;
(3) 求平面PAD与平面PBC所成锐二面角的正切值。
求平面PAD与平面PBC所成锐二面角的正切值。
(本小题满分12分)已知圆 的圆心为原点,且与直线
的圆心为原点,且与直线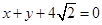 相切。
相切。
(1)求圆 的方程;
的方程;
(2)点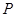 在直线
在直线 上,过
上,过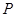 点引圆
点引圆 的两条切线
的两条切线 ,切点为
,切点为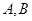 ,求证:直线
,求证:直线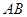 恒过定点。
恒过定点。
(本小题满分12分)已知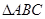 的顶点
的顶点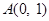 ,
,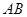 边上的中线
边上的中线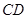 所在的直线方程为
所在的直线方程为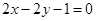 ,
,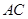 边上的高
边上的高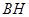 所在直线的方程为
所在直线的方程为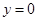 .
.
(1)求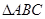 的顶点
的顶点 、
、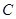 的坐标;
的坐标;
(2)若圆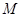 经过
经过 、
、 且与直线
且与直线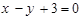 相切于点
相切于点 (-3,0),求圆
(-3,0),求圆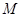
 的方程.
的方程.
.本小题满分12分)如图(1),边长为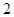 的正方形
的正方形 中,
中,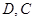 分别为
分别为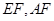 上的点,且
上的点,且 ,现沿
,现沿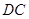 把
把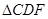 剪切、拼接成如图(2)的图形,再将
剪切、拼接成如图(2)的图形,再将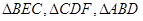 沿
沿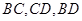 折起,使
折起,使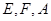 三点重合于点
三点重合于点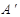 。
。
(1)求证: ;
;
(2)求四面体 体积的最大值。
体积的最大值。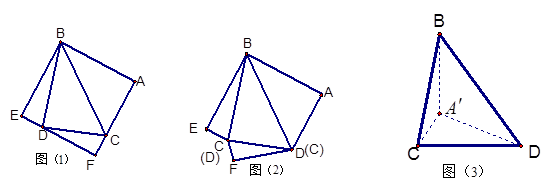
.(本小题满分10分)已知不等式 的解集为
的解集为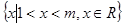
(1)求 、
、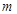 的值;
的值;
(2)若函数 在区间
在区间 上递增,求关于
上递增,求关于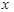 的不等式
的不等式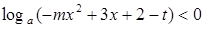 的解集。
的解集。