已知函数 ,其中
,其中 且m为常数.
且m为常数.
(1)试判断当 时函数
时函数 在区间
在区间 上的单调性,并证明;
上的单调性,并证明;
(2)设函数 在
在 处取得极值,求
处取得极值,求 的值,并讨论函数
的值,并讨论函数 的单调性.
的单调性.
选修4-4:坐标系与参数方程)已知极坐标系的极点与直角坐标系的原点重合,极轴与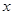 轴的正半轴重合.若直线
轴的正半轴重合.若直线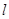 的极坐标方程为
的极坐标方程为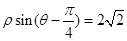 .
.
(1)把直线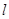 的极坐标方程化为直角坐标系方程;
的极坐标方程化为直角坐标系方程;
(2)已知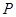 为椭圆
为椭圆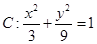 上一点,求
上一点,求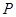 到直线
到直线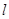 的距离的最小值.
的距离的最小值.
(选修4-2:矩阵与变换) 已知矩阵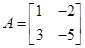 , (1)求逆矩阵
, (1)求逆矩阵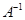 ;(2)若矩阵
;(2)若矩阵 满足
满足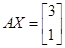 ,试求矩阵
,试求矩阵 .
.
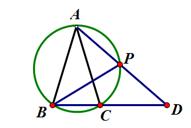
(选修4-1:几何证明选讲)如图在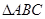 中,AB=AC,过点A的直线与
中,AB=AC,过点A的直线与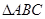 的外接圆交于点P,交BC的延长线于点D.求证
的外接圆交于点P,交BC的延长线于点D.求证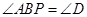
(本小题满分16分)已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn.求满足不等式>2 010的n的最小值.
(本小题满分16分)已知函数 ,函数
,函数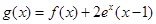 ,函数
,函数
(1)当函数 在
在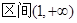 时为减函数,求a的范围;
时为减函数,求a的范围;
(2)若a=e(e为自然对数的底数);
①求函数g(x)的单调区间;
②证明: