某单位有车牌尾号为2的汽车A和尾号为6的汽车B,两车分属于两个独立业务部门.对一段时间内两辆汽车的用车记录进行统计,在非限行日,A车日出车频率0.6,B车日出车频率0.5.该地区汽车限行规定如下:
| 车尾号 |
0和5 |
1和6 |
2和7 |
3和8 |
4和9 |
| 限行日 |
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
现将汽车日出车频率理解为日出车概率,且A,B两车出车相互独立.
(1)求该单位在星期一恰好出车一台的概率;
(2)设X表示该单位在星期一与星期二两天的出车台数之和,求X的分布列及其数学期望E(X).
(本小题满分16分)
某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其在
40分钟的一节课中,注意力指数p与听课时间t(单位:分钟)之间的关系满足如图
所示的曲线.当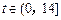 时
时 ,曲线是二次函数图象的一部分,当
,曲线是二次函数图象的一部分,当 时,曲线
时,曲线
是函数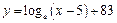 (
(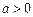 ,
,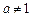 )图象的一部分.根据专家研究,当注意力指数p大于80时学习效果最佳.
)图象的一部分.根据专家研究,当注意力指数p大于80时学习效果最佳.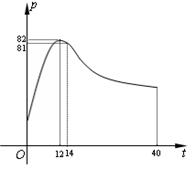
(1)试求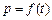 的函数关系式;
的函数关系式;
(2)教师在什么时段内安排核 心内容,能使得学生学习效果最佳?请说明理由.
心内容,能使得学生学习效果最佳?请说明理由.
(本小题满分16分)
已知函数 ,且对于任意
,且对于任意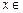 R,恒有
R,恒有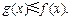
(1)证明: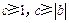 ;
;
(2)设函数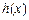 满足:
满足: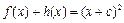 ,证明:函数
,证明:函数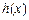 在
在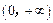 内没有零点.
内没有零点.
(本小题满分14分)
设函数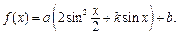
(1)当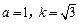 时,求函数
时,求函数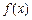 的单调减区间;
的单调减区间;
(2)当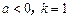 时,函数
时,函数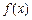 在
在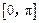 上的值域是[2,3],求a,b的值.
上的值域是[2,3],求a,b的值.
(本小题满分14分)
已知向量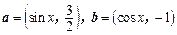 .
.
(1)当a//b时,求 的值;
的值;
(2)设函数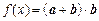 ,问:由函数
,问:由函数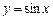 的图象经过怎样的变换可得函数
的图象经过怎样的变换可得函数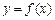 的图象?
的图象?
(本小题满分14分)
设集合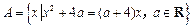 ,
,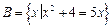 .
.
(1)若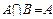 ,求实数
,求实数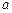 的值;
的值;
(2)求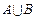 ,
,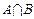 .
.