(本小题满分14分)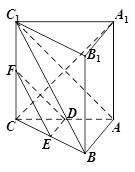
如图,在三棱柱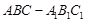 中,
中, 底面
底面 ,
,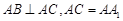 ,E、F分别是棱
,E、F分别是棱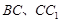 的中点.
的中点.
(1)求证:AB⊥平面AA1 C1C;
(2)若线段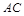 上的点
上的点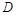 满足平面
满足平面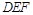 //平面
//平面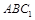 ,试确定点
,试确定点 的位置,并说明理由;
的位置,并说明理由;
(3)证明: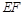 ⊥A1C.
⊥A1C.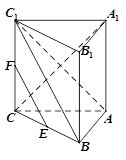
已知中心在原点的椭圆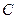 的右焦点为
的右焦点为 ,离心率为
,离心率为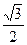
(1)求椭圆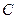 的方程
的方程
(2)若直线 :
: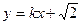 与椭圆
与椭圆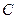 恒有两个不同交点
恒有两个不同交点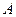 、
、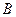 ,且
,且 (其中
(其中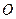 为原点),求实数
为原点),求实数 的取值范围
的取值范围
已知定义在(0,+ )上的函数
)上的函数 是增函数
是增函数
(1)求常数 的取值范围
的取值范围
(2)过点(1,0)的直线与 (
( )的图象有交点,求该直线的斜率的取值范围
)的图象有交点,求该直线的斜率的取值范围
如图,正四棱柱 中,
中, ,点
,点 在
在 上且
上且
(1)证明: 平面
平面 ;(2)求二面角
;(2)求二面角 的余弦值
的余弦值
已知函数 (
(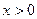 )在
)在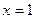 处取得极值
处取得极值 ,其中
,其中 为常数
为常数
(1)求 的值;(2)讨论函数
的值;(2)讨论函数 的单调区间
的单调区间
(3)若对任意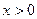 ,
, 恒成立,求
恒成立,求 的取值范围
的取值范围
已知甲盒内有大小相同的1个红球和3个黑球, 乙盒内有大小相同的2个红球和4个黑球,现从甲乙两个盒中各任取2球
(1)求取出的4个球均为黑球的概率
(2)求取出的4个球中恰有1个红球的概率
(3)设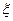 为取出的4个球中红
为取出的4个球中红 球的个数,求
球的个数,求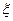 的分布列和数学期望
的分布列和数学期望