已知中心在原点的椭圆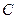
的右焦点为
，离心率为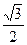
（1） 求椭圆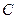的方程
（2） 若直线
：
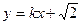与椭圆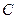恒有两个不同交点
、
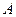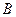，且
（其中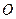
为原点），求实数
的取值范围
已知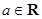
，函数
．
（1）若函数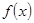
在区间
内是减函数，求实数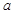
的取值范围；
（2）求函数
在区间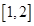
上的最小值
；
已知函数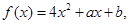
.设关于x的不等式
的解集为
且方程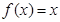
的两实根为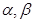
.
（1）若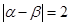
，求
的关系式；
（2）若
，求
的范围。
已知函数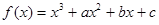
在x=
与x =l时都取得极值
（1）求a、b的值与函数f（x）的单调区间
（2）若对x∈（-1，2），不等式f（x）<c2恒成立，求c的取值范围。
某产品在一个生产周期内的总产量为100t，平均分成若干批生产。设每批生产需要投入固定费用75元，而每批生产直接消耗的费用与产品数量x的平方成正比，已知每批生产10t时，直接消耗的费用为300元（不包括固定的费用）。
（1）若每批产品数量为20t,求此产品在一个生产周期的总费用（固定费用和直接消耗的费用）。
（2）设每批产品数量为xt，一个生产周期内的总费用y元，求y与x的函数关系式，并求
出y的最小值。
命题p：函数
有零点；
命题q：函数
是增函数，
若命题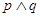
是真命题，求实数
的取值范围．