甲、乙两人参加某种选拔测试.在备选的10道题中,甲答对其中每道题的概率都是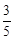
,乙能答对其中5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
（1）求乙得分的分布列和数学期望；
（2）求甲、乙两人中至少有一人入选的概率.
已知
的顶点A、B在椭圆
,点
在直线
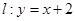上，且
（1）当AB边通过坐标原点O时，求的面积；
（2）当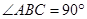
，且斜边AC的长最大时，
求AB所在直线的方程。
如图，A，B，C三个观察哨，A在B的正南，两地相距6km，C在B的北偏东60°，两地相距4km.在某一时刻，A观察哨发现某种信号，并知道该信号的传播速度为1km/s；4秒后B,C两个观察哨同时发现这种信号。在以过A,B两点的直线为y轴，以线段AB的垂直平分线为x轴的平面直角坐标系中，指出发了这种信号的地点P的坐标。
在直角坐标系
中，点P是曲线C上任意一点，点P到两点
，
的距离之和等于4，直线
与C交于A，B两点．
（Ⅰ）写出C的方程；
（Ⅱ）若
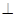
，求k的值。
已知二次函数
(
是常数，且
)满足条件：
，且方程
有两个相等实根．
(1)求
的解析式；
(2)是否存在实数
，使的定义域和值域分别为
和
？若存在，求出
的值；若不存在，说明理由．
在经济学中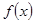，函数
的边际函数
定义为
。某公司每月最多生产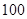
台报警系统装置，生产
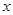台的收入函数为
（单位：元），其成本函数为
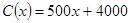（单位：元），利润是收入与成本之差。
(1)求利润函数
及边际利润函数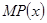
；
(2)利润函数与边际利润函数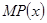是否具有相等的最大值
(3)你认为本题中边际利润函数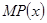取最大值的实际意义是什么？