如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=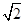 .
.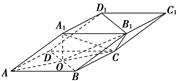
(1)证明:A1C⊥平面BB1D1D;
(2)求平面OCB1与平面BB1D1D的夹角θ的大小.
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位辆),若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆
| 轿车A |
轿车B |
轿车C |
|
| 舒适型 |
100 |
150 |
z |
| 标准型 |
300 |
450 |
600 |
(1)求下表中z的值;
(2)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:94,86,92,96,87,93,90,82把这8辆轿车的得分看作一个总体,从中任取一个得分数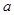 记这8辆轿车的得分的平均数为
记这8辆轿车的得分的平均数为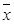 ,定义事件
,定义事件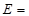 {
{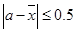 ,且函数
,且函数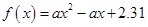 没有零点},求事件
没有零点},求事件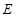 发生的概率
发生的概率
在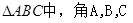 所对的边分别为
所对的边分别为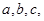 且
且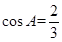 .
.
(1)求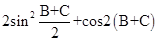 ;
;
(2)若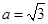 ,求
,求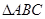 面积的最大值.
面积的最大值.
已知函数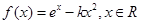 .
.
(1)若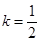 ,求证:当
,求证:当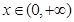 时,
时,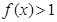 ;
;
(2)若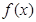 在区间
在区间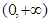 上单调递增,试求
上单调递增,试求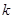 的取值范围;
的取值范围;
(3)求证: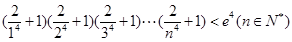 .
.
已知中心在原点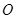 的椭圆C:
的椭圆C: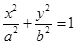 的一个焦点为F1(0,3),M(x,4)(x>0)为椭圆C上一点,△MOF1的面积为
的一个焦点为F1(0,3),M(x,4)(x>0)为椭圆C上一点,△MOF1的面积为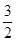 .
.
(1) 求椭圆C的方程;
(2) 是否存在平行于OM的直线l,使得直线l与椭圆C相交于A,B两点,且以线段AB为直径的圆恰好经过原点?若存在,求出直线l的方程;若不存在,说明理由.
如图,四棱锥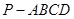 中,底面
中,底面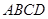 为直角梯形,
为直角梯形,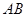 ∥
∥ ,
, 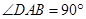 ,
,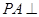 平面
平面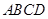 ,且
,且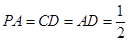 ,
,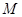 为
为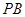 的中点
的中点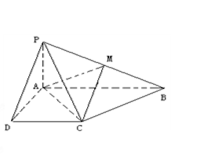
(1) 证明:面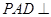 面
面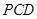
(2) 求面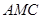 与面
与面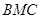 夹角的余弦值.
夹角的余弦值.