已知数列{an}的前n项和为Sn,且Sn=2an-2,数列{bn}满足b1=1,且bn+1=bn+2.
(1)求数列{an},{bn}的通项公式;
(2)设cn=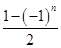 an-
an-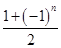 bn,求数列{cn}的前2n项和T2n.
bn,求数列{cn}的前2n项和T2n.
如图 ,在四棱锥S—ABCD中,底面ABCD为矩形,SA⊥平面ABCD,SA=AD,M为AB中点,N为SC中点.
,在四棱锥S—ABCD中,底面ABCD为矩形,SA⊥平面ABCD,SA=AD,M为AB中点,N为SC中点.
(1)证明:MN//平面SAD;
(2)证明:平面SMC⊥平面SC D;
D;
已知三次函数 =
= ,
, 、
、 为实数,
为实数, =1,
=1,
曲线y= 在点(1,
在点(1, )处切线的斜率为-6。
)处切线的斜率为-6。
(1)求函数 的解析式;
的解析式;
(2)求函数 在(-2,2)上的最大值
在(-2,2)上的最大值
(本小题满分12分)对某班级50名同学一年来参加社会实践的次数进行的调查
统计,得到如下频率分布表:
| 参加次数 |
0 |
1 |
2 |
3 |
| 人数 |
0.1 |
0.2 |
0.4 |
0.3 |
根据上表信息解答以下问题: 
(本小题满分14分)(1)
(本小题满分7分)选修4-2:矩阵与变换
已知曲线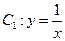 绕原点逆时针旋转
绕原点逆时针旋转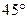 后可得到曲线
后可得到曲线 ,
,
(I)求由曲线 变换到曲线
变换到曲线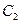 对应的矩阵
对应的矩阵 ;.
;.
(II)若矩阵 ,求曲线
,求曲线 依次经过矩阵
依次经过矩阵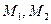 对应的变换
对应的变换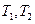 变换后得到的曲线方程.
变换后得到的曲线方程.
(2)(本小题满分7分)选修4—4:坐标系与参数方程
已知直线 的参数方程为
的参数方程为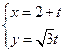 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为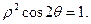
(1)求曲线C的直角坐标方程;(2)求直线 被曲线C截得的弦长.
被曲线C截得的弦长.
(本小题满分12分)
(1)(本小题满分5分)选修4-2:矩阵与变换。已知矩阵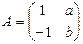 ,A的一个特征值
,A的一个特征值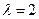 ,属于λ的特征向量是
,属于λ的特征向量是 ,求矩阵A与其逆矩阵.
,求矩阵A与其逆矩阵.
(2) (本小题满分7分)选修4—4:坐标系与参数方程
已知直线 的极坐标方程是
的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为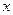 轴的正半轴,建立平面直角坐标系,在曲线
轴的正半轴,建立平面直角坐标系,在曲线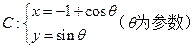 上求一点,使它到直线
上求一点,使它到直线 的距离最小,并求出该点坐标和最小距离.
的距离最小,并求出该点坐标和最小距离.