已知向量a=(cos 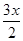 ,sin
,sin 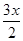 ),b=(-sin
),b=(-sin 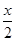 ,-cos
,-cos 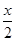 ),其中x∈[
),其中x∈[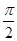 ,π].
,π].
(1)若|a+b|= ,求x的值;
,求x的值;
(2)函数f(x)=a·b+|a+b|2,若c>f(x)恒成立,求实数c的取值范围.
(本小题满分12分)如图所示,四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=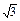 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.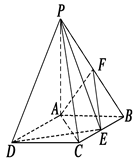
(1)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)求证:无论点E在BC边的何处,都有PE⊥AF;
(3)当BE为何值时,PA与平面PDE所成角的大小为45°.
、(本小题满分12分)某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置. 若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.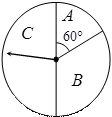
(1)若某位顾客消费128元,求返券金额不低于30元的概率;
(2)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为 (元).求随机变量
(元).求随机变量 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)已知:正项数列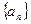 的前
的前 项和为
项和为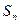 ,方程
,方程 有一根为
有一根为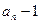
(1)求数列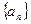 的通项
的通项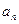 .
.
(2)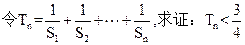 .
.
(本小题满分12分)已知向量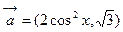 ,
,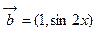 ,函数
,函数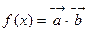 ,
,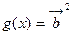 .
.
(1)求函数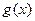 的最小正周期;
的最小正周期;
(2)在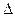
 中,
中,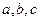 分别是角
分别是角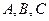 的对边,且
的对边,且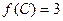 ,
,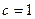 ,
,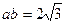 ,且
,且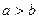 ,求
,求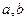 的值.
的值.
、(本小题满分14分)已知点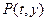 在函数
在函数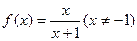 的图象上,且有
的图象上,且有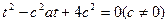 .
.
(1) 求证: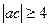 ;
;
(2) 求证:在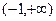 上
上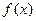 单调递增.
单调递增.
(3) 求证: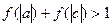 .
.