重庆一中渝北校区为奖励“我的中国梦”寒假系列实践活动的获奖学生，学校准备在某商店购买A，B两种文具作为奖品，已知一件A种文具的单价比B种文具的单价便宜4元，而用300元买A种文具的件数是用200元买B种文具的件数的2倍.
（1）求A种文具的单价；
（2）根据需要，学校准备在该商店购买A，B两种文具共200件，其中A种文具的件数不多于B种文具件数的3倍.为了节约经费，当购买A，B两种文具各多少件时，所用经费最少？最少经费为多少元？
10月国庆佳节，景山旅行社为吸引游客组团去具有喀斯特地貌特征的黄果树风景区旅游，推出了如下收费标准（如图所示）：
某单位组织员工去具有喀斯特地貌特征的黄果树风景区旅游，共支付给旅行社旅游费用27000元，请问该单位这次共有多少名员工去具有喀斯特地貌特征的黄果树风景区旅游？
已知：
ABCD的两边AB，AD的长是关于x的方程
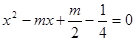的两个实数根．
（1）当m为何值时，四边形ABCD是菱形？求出这时菱形的边长；
（2）若AB的长为2，那么
ABCD的周长是多少？
已知关于x的方程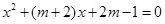
．
（1）求证：方程有两个不相等的实数根；
（2）是否存在实数m，使方程的两个实数根互为相反数?若存在，求出m的值；若不存在，说明理由．
如图，在Rt△ABC中，∠ACB=90°，以AC为直径作⊙O交AB于点D，连接CD．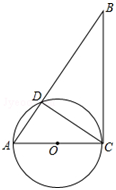
（1）求证：∠A=∠BCD；
（2）若M为线段BC上一点，试问当点M在什么位置时，直线DM与⊙O相切？并说明理由．
如图，AB与
相切于C，
，的半径为6，OA＝10，求AB的长．