从某学校的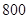 名男生中随机抽取
名男生中随机抽取 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于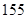 cm和
cm和 cm之间,将测量结果按如下方式分成八组:第一组[
cm之间,将测量结果按如下方式分成八组:第一组[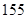 ,
,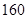 ),第二组[
),第二组[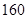 ,
, ),…,第八组[
),…,第八组[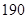 ,
, ],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为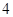 人.
人.
(1)求第七组的频率并估计该校800名男生中身高在 cm以上(含
cm以上(含 cm)的人数;
cm)的人数;
(2)从第六组和第八组的男生中随机抽取两名男生,记他们的身高分别为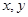 ,事件
,事件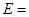 {
{ },求
},求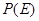 .
.
已知双曲线的中心在原点,焦点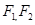 在坐标轴上,离心率为
在坐标轴上,离心率为 ,且过点
,且过点
(1)求双曲线的方程.
(2)若点
(3)在(2)的条件下
求满足下列条件的曲线方程
(1)经过两点P( ,1),Q(
,1),Q(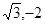 )的椭圆的标准方程.
)的椭圆的标准方程.
(2)与双曲线 有共同的渐近线,且经过点
有共同的渐近线,且经过点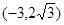 的双曲线的标准方程.
的双曲线的标准方程.
(3)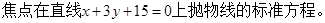
设函数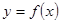 定义在
定义在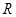 上,对于任意实数
上,对于任意实数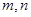 ,恒有
,恒有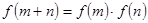 ,且当
,且当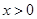 时,
时,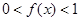
(1)求证: 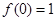 且当
且当 时,
时,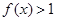
(2)求证: 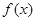 在
在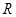 上是减函数;
上是减函数;
(3)设集合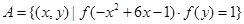 ,
,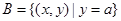 ,且
,且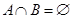 ,
,
求实数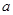 的取值范围。
的取值范围。
某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需要增加投入100元,已知总收益满足函数: ,其中
,其中 是仪器的月产量。
是仪器的月产量。
(1)将利润 元表示为月产量
元表示为月产量 台的函数;
台的函数;
(2)当月产量为何值时,公司所获得利润最大?最大利润是多少?(总收益=总成本+利润).
已知函数 .
.
(1)证明:不论 为何实数
为何实数 总为增函数
总为增函数
(2)确定 的值, 使
的值, 使 为奇函数;
为奇函数;
(3)当 为奇函数时, 求
为奇函数时, 求 的值域.
的值域.