如图所示，竖直面内有一倒立等边三角形OMN区域，连长为L，MN边是水平的。在该区域有一垂直纸面向外磁感应强度为B的匀强磁场。在同一竖直面内有一束质量为m、电荷量为q、速度大小不同的带正电粒子从N点沿NM方向射入该磁场区域（可认为能发生偏转）。过O点作与MN边平行的直线作为X坐标轴，且O点为X坐标轴的原点。不计粒子的重力及粒子间的相互作用力，试求：
⑴射到X坐标轴上的O点的粒子速度大小；
⑵垂直OM边射出的粒子与X坐标轴的交点位置；
⑶粒子在磁场中运动的时间和速度的关系。
如图所示,BC为半径等于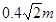
竖直放置的光滑细圆管，O为细圆管的圆心，在圆管的末端C连接倾斜角为450、
的足够长粗糙斜面，一质量为m=0.5kg的小球从O点正上方某处A点以V0水平抛出，恰好能垂直OB从B点进入细圆管，小球从进入圆管开始受到始终竖直向上的力F=5N的作用，当小球运动到圆管的末端C时作用力F立即消失，能平滑的冲上粗糙斜面。（g=10m/s2）
求：
（1）小球从O点的正上方某处A点水平抛出的初速度v0为多少？
（2）小球在圆管中运动对圆管的压力是多少？
（3）小球在CD斜面上运动的最大位移是多少？
某课外小组经长期观测，发现靠近某行星周围有众多卫星，且相对均匀地分布于行星周围，假设所有卫星绕该行星的运动都是匀速圆周运动，通过天文观测，测得离行星最近的一颗卫星的运动半径为R1，周期为T1，已知万有引力常为G。求：
（1）若行星的半径为R，行星的第一宇宙速度；
（2）通过天文观测，发现离行星很远处还有一颗卫星，其运动半径为R2，周期为T2，试估算靠近行星周围众多卫星的总质量。
开普勒定律不仅适用于太阳系，它对一切具有中心天体的引力系统(如地月系统)都成立．经测定月地距离为3.84×108m，月球绕地球运动的周期为2.36×106s，试计算地球的质量M地. (G＝6.67×10－11N·m2/kg2，结果保留一位有效数字)
一质量为2000 kg的汽车，行驶到一座半径为40m的圆弧形拱桥顶端时，汽车运动速度为8m/s。求此时汽车对桥面的压力的大小（g=10m/s2）。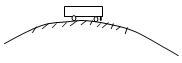
在xoy平面内，直线OP与y轴的夹角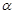
=45o。第一、第二象限内存在大小相等，方向分别为竖直向下和水平向右的匀强电场,电场强度E=1.0×105N/C ；在x轴下方有垂直于纸面向外的匀强磁场，磁感应强度B=0.1T，如图所示。现有一带正电的粒子从直线OP上某点A（-L, L）处静止释放。设粒子的比荷
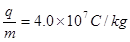，粒子重力不计。求：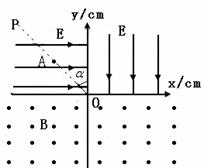
（1）当L=2cm时，粒子进入磁场时与x轴交点的横坐标
（2）当L=2cm时，粒子进入磁场时速度的大小和方向
（3）如果在直线OP上各点释放许多个上述带电粒子（粒子间的相互作用力不计），试证明各带电粒子进入磁场后做圆周运动的圆心点的集合为一抛物线（提示：写出圆心点坐标x、y的函数关系）