如图,椭圆的离心率为,轴被曲线截得的线段长等于的长半轴长。

(1)求,的方程;
(2)设与轴的交点为,过坐标原点的直线与相交于点,直线分别与相交与.
①证明:;
②记的面积分别是.问:是否存在直线,使得=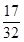 ?请说明理由。
?请说明理由。
已知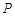 :
: ,
,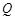 :
: .
.
(1)若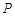 是
是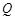 充分不必要条件,求实数
充分不必要条件,求实数 的取值范围;
的取值范围;
(2)若“非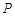 ”是“非
”是“非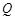 ”的充分不必要条件,求实数
”的充分不必要条件,求实数 的取值范围.
的取值范围.
已知直线l:kx-y+1+2k=0.
(1)求证:直线l过定点;
(2)若直线l交x轴负半轴于点A,交y正半轴于点B,△AOB的面积为S,试求S的最小值并求出此时直线l的方程.
已知两点A(-1,2)、B(m,3).
(1)求直线AB的方程;
(2)已知实数m∈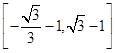 ,求直线AB的倾斜角α的取值范围.
,求直线AB的倾斜角α的取值范围.
设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(1)若l在两坐标轴上截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
已知△ABC中,A(1,-4),B(6,6),C(-2,0).求:
(1)△ABC中平行于BC边的中位线所在直线的一般式方程和截距式方程;
(2)BC边的中线所在直线的一般式方程,并化为截距式方程.