如图,从点作轴的垂线交曲线于点,曲线在点处的切线与轴交于点.再从做轴的垂线交曲线于点,依次重复上述过程得到一系列点:;;…;,记点的坐标为().

(1)试求与的关系();
(2)求.
已知抛物线的方程为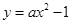 ,直线
,直线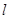 的方程为
的方程为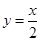 ,点
,点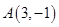 关于直线
关于直线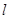 的对称点在抛物线上.
的对称点在抛物线上.
(1)求抛物线的方程;
(2)已知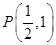 ,求过点
,求过点 及抛物线与
及抛物线与 轴两个交点的圆的方程;
轴两个交点的圆的方程;
(3)已知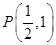 ,点
,点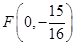 是抛物线的焦点,
是抛物线的焦点,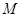 是抛物线上的动点,求
是抛物线上的动点,求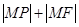 的最小值及此时点
的最小值及此时点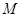 的坐标;
的坐标;
如图,已知三棱柱 的侧棱与底面垂直,且
的侧棱与底面垂直,且 ,
, ,
, ,
, ,点
,点 、
、 、
、 分别为
分别为 、
、 、
、 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: 面
面 ;
;
(3)求点 到平面
到平面 的距离.
的距离.
下表是某市从3月份中随机抽取的 天空气质量指数(
天空气质量指数( )和“
)和“ ”(直径小于等于
”(直径小于等于 微米的颗粒物)
微米的颗粒物) 小时平均浓度的数据,空气质量指数(
小时平均浓度的数据,空气质量指数( )小于
)小于 表示空气质量优良.
表示空气质量优良.
| 日期编号 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
空气质量指数( ) ) |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
“ ” ” 小时平均浓度( 小时平均浓度( ) ) |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
(1)根据上表数据,估计该市当月某日空气质量优良的概率;
(2)在上表数据中,在表示空气质量优良的日期中,随机抽取两个对其当天的数据作进一步的分析,设事件 为“抽取的两个日期中,当天‘
为“抽取的两个日期中,当天‘ ’的
’的 小时平均浓度不超过
小时平均浓度不超过 ”,求事件
”,求事件 发生的概率.
发生的概率.
在 中,已知
中,已知 ,
, 且
且 .
.
(1)求角 和
和 的值;
的值;
(2)若 的边
的边 ,求边
,求边 的长.
的长.
已知函数 ,
, (
( 为常数).
为常数).
(1)函数 的图象在点
的图象在点 处的切线与函数
处的切线与函数 的图象相切,求实数
的图象相切,求实数 的值;
的值;
(2)若 ,
, ,
, 、
、 使得
使得 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数 ;
;
(3)当 时,若对于区间
时,若对于区间 内的任意两个不相等的实数
内的任意两个不相等的实数 、
、 ,都有
,都有
 成立,求
成立,求 的取值范围.
的取值范围.