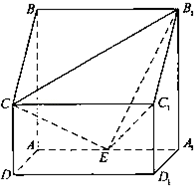
如图,四棱柱中,侧棱,,,,,为棱的中点.
(1)证明;
(2)求二面角的正弦值.
(3)设点在线段上,且直线与平面所成角的正弦值为,求线段的长.
直线l经过P(2,3),且在x,y轴上的截距相等,试求该直线方程.
已知正方形ABCD 对角线AC所在直线方程为 .抛物线
.抛物线 过B,D两点
过B,D两点
(1)若正方形中心M为(2,2)时,求点N(b,c)的轨迹方程。
(2)求证方程 的两实根
的两实根 ,
, 满足
满足
如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为 的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点,求△AMN面积最大时直线l的方程,并求△AMN的最大面积
的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点,求△AMN面积最大时直线l的方程,并求△AMN的最大面积
如图,已知某椭圆的焦点是F1(-4,0)、F2(4,0),过点F2并垂直于x轴的直线与椭圆的一个交点为B,且|F1B|+|F2B|=10,椭圆上不同的两点A(x1,y1),C(x2,y2)满足条件|F2A|、|F2B|、|F2C|成等差数列(1)求该弦椭圆的方程;(2)求弦AC中点的横坐标;(3)设弦AC的垂直平分线的方程为y=kx+m,求m的取值范围
如图:在面积为1的DPMN中,tanÐPMN= ,tanÐMNP=-2,试建立适当的坐标系,求以M、N为焦点且过点P的椭圆方程。
,tanÐMNP=-2,试建立适当的坐标系,求以M、N为焦点且过点P的椭圆方程。