在2014年全国超级联赛上,兵乓球比赛团体决赛实行五场三胜制,且任何一方获胜三场比赛即结束.甲,乙两个代表队最终进入决赛,根据双方排定的出场顺序及以往战绩统计分析,甲队依次派出的五位选手分别战胜对手的概率如下表:
| 出场顺序 |
1号 |
2号 |
3号 |
4号 |
5号 |
| 获胜概率 |
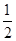 |
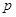 |
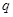 |
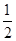 |
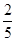 |
若甲队横扫对手获胜(即3:0获胜)的概率是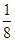 ,比赛至少打满4场的概率为
,比赛至少打满4场的概率为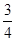
(Ⅰ)求 的值
的值
(Ⅱ)求甲队获胜场数的分布列和数学期望
已知 ,
, ,(1)若
,(1)若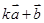 与
与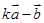 垂直,求
垂直,求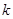 的值;(2)若
的值;(2)若 ,求
,求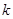 的值.
的值.
已知数列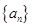 中,
中,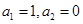 其前
其前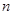 项和
项和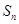 满足:
满足: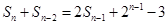

(1)试求数列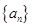 的通项公式;
的通项公式;
(2)求数列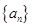 的前
的前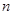 项和
项和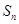 .
.
正项数列 的前
的前 项和
项和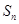 满足:
满足:
(1)求数列 的通项公式;
的通项公式;
(2)令 ,求数列
,求数列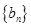 的前
的前 项和
项和 .
.
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度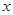 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当 时,车流速度
时,车流速度 是车流密度
是车流密度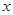 的一次函数.
的一次函数.
(1)当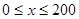 时,求函数
时,求函数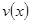 的表达式;
的表达式;
(2)当车流密度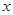 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)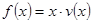 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)
在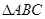 中,角
中,角 的对边分别为
的对边分别为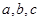 .已知
.已知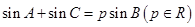 ,且
,且 .
.
(1)当 时,求
时,求 的值;
的值;
(2)若角 为锐角,求
为锐角,求 的取值范围.
的取值范围.