某种汽车购买时费用为 万元,每年应交保险费,养路费,保险费共
万元,每年应交保险费,养路费,保险费共 万元,汽车的维修费为:第一年
万元,汽车的维修费为:第一年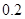 万元,第二年
万元,第二年 万元,第三年
万元,第三年 万元,……,依次成等差数列逐年递增.
万元,……,依次成等差数列逐年递增.
(1)设使用 年该车的总费用(包括购车费用)为
年该车的总费用(包括购车费用)为 试写出
试写出 的表达式;
的表达式;
(2)求这种汽车使用多少年报废最合算(即该车使用多少年平均费用最少).
如图,已知点D(0,-2),过点D作抛物线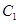 :
: 的切线l,切点A在第二象限。
的切线l,切点A在第二象限。
(1)求切点A的纵坐标;
(2)若离心率为 的椭圆
的椭圆 恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k,
恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k,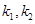 ,①试用斜率k表示
,①试用斜率k表示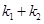 ②当
②当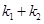 取得最大值时求此时椭圆的方程。
取得最大值时求此时椭圆的方程。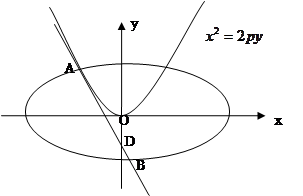
2012年春晚歌舞类节目成为春晚顶梁柱,尤其是不少创意组合都被网友称赞很有新意。王力宏和李云迪的钢琴PK,加上背景板的黑白键盘,更被网友称赞是行云流水的感觉。某网站从2012年1月23号到1月30做了持续一周的在线调查,共有n人参加调查,现将数据整理分组如题中表格所示。
| 序号 |
年龄分组 |
组中值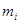 |
频数(人数) |
频率(f) |
| 1 |
[20,25) |
22.5 |
x |
s |
| 2 |
[25,30) |
27.5 |
800 |
t |
| 3 |
[30,35) |
32.5 |
y |
0.40 |
| 4 |
[35,40) |
37.5 |
1600 |
0.32 |
| 5 |
[40,45) |
42.5 |
z |
0.04 |
(1)求n及表中x,y,z,s,t的值
(2)为了对数据进行分析,采用了计算机辅助计算,分析其中一部分计算,见算法流程图,求输出的S值,并说明S的统计意义。
(3)从年龄在[20,30)岁人群中采用分层抽样法抽取6人参加元宵晚会活动,其中选取2人作为代表发言,求选取2名代表中恰有1人年龄在[25,30)岁的概率。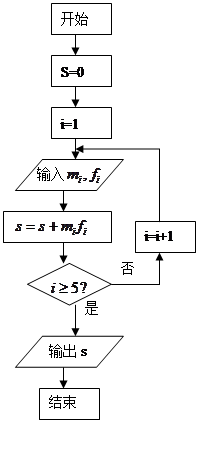
已知公差不为0的等差数列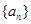 的前3项和
的前3项和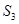 =9,且
=9,且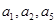 成等比数列。
成等比数列。
(1)求数列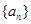 的通项公式和前n项和
的通项公式和前n项和
(2)设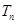 为数列
为数列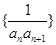 的前n项和,若
的前n项和,若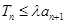 对一切
对一切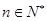 恒成立,求实数
恒成立,求实数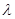 的最小值。
的最小值。
已知向量 ,设函数
,设函数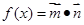 +
+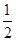
(1)若 ,f(x)=
,f(x)=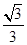 ,求
,求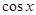 的值;
的值;
(2)在△ABC中,角A,B,C的对边分别是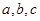 ,且满足
,且满足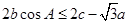 ,求f(B)的取值范围.
,求f(B)的取值范围.
(1)证明不等式: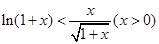
(2)已知函数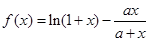 在
在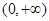 上单调递增,求实数
上单调递增,求实数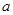 的取值范围。
的取值范围。
(3)若关于x的不等式 在
在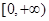 上恒成立,求实数
上恒成立,求实数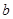 的最大值。
的最大值。