已知向量m=( sin
sin 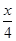 ,1),n=(cos
,1),n=(cos 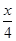 ,cos2
,cos2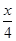 ).记f(x)=m·n.
).记f(x)=m·n.
(1)若f(α)=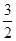 ,求cos(
,求cos( -α)的值;
-α)的值;
(2)在△ABC中,角A、B、C的对边分别是a、b、c,且满足(2a-c)cos B=bcos C,若f(A)=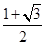 ,试判断△ABC的形状.
,试判断△ABC的形状.
各棱长均为2的斜三棱柱ABC—DEF中,已知BF⊥AE,
BF∩CE=O,AB=AE,连结AO。
(I)求证:AO⊥平面FEBC。
(II)求二面角B—A C—E的大小。
C—E的大小。
(III)求三棱锥B—DEF的体积。
(本小题满分13分)
我校要用三辆汽车把高二文科学生从学校送到古田参加社会实践活动,已知学校到古田有两条公路,汽车走公路①堵车的概率为 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为 ,不堵车的概率为
,不堵车的概率为 .若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响
.若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响
(I)若三辆汽车中恰有一辆汽车被堵的概率为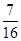 ,求汽
,求汽 车走公路②堵车的概率P。
车走公路②堵车的概率P。
(II)在(1)的条件下,求三辆汽车中被堵车辆的个数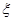 的分布列和数学期望。
的分布列和数学期望。
在ΔABC中,角A、B、C所对的边分别为a、b、c,且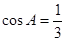 。
。
(I)求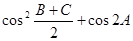 的值。
的值。
(II)若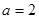 ,
,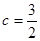 ,求∠C。
,求∠C。
(本小题满分12分)
如图,已知椭圆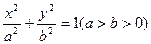 的离心率为
的离心率为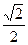 ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点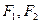 为顶点的三角形的周长为
为顶点的三角形的周长为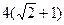 ,一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于项点的任一点,直线
,一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于项点的任一点,直线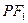 和
和 与椭圆的交点分别为A、B和C、D.
与椭圆的交点分别为A、B和C、D.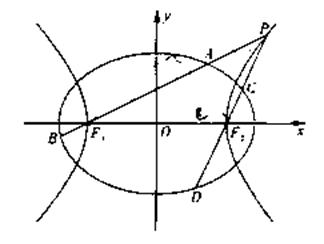
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线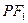 、
、 的斜率分别为
的斜率分别为 、
、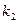 ,证明:
,证明: ;
;
(Ⅲ)是否存在常数 ,使得
,使得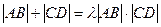 恒成立?若存在,求
恒成立?若存在,求 的值;若不存在,请说
的值;若不存在,请说 明理由.
明理由.
两定点的坐标分别A(-1,0),B(2,0),动点M满 足条件
足条件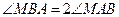 ,求动
,求动 点M的轨迹方程并指出轨迹是什么图形
点M的轨迹方程并指出轨迹是什么图形