假设某班级教室共有4扇窗户，在每天上午第三节课上课预备铃声响起时，每扇窗户或被敞开或被关闭，且概率均为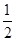
，记此时教室里敞开的窗户个数为X．
(1)求X的分布及数学期望；
(2)若此时教室里有两扇或两扇以上的窗户被关闭，班长就会将关闭的窗户全部敞开，否则维持原状不变．记每天上午第三节课上课时该教室里敞开的窗户个数为Y，求Y的数学期望．
（本小题满分12分）已知数列
是首项
的等差数列，其前n项和为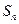
，
数列
是首项
的等比数列，且
（1）求
（2）令
，若数列
的前n项和为
，试比较
的大小。
（本小题满分12分）已知函数
，其中
（1）若
为偶函数，求a的值；
（2）命题p：函数
上是增函数，命题q：函数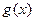
是减函数，如果p或q为真，p且q为假，求a的取值范围。
（3）在（2）的条件下，比较
的大小。
（本小题满分12分）已知函数
，且函数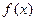
的最小正周期为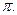
（1）若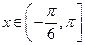
，求函数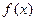的单调递减区间；
（2）将函数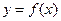
的图象上各点的纵坐标保持不变，横坐标缩短到原来的
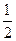，把所得到的图象再向左平移
个单位，得到函数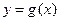
的图象，求函数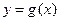在区间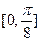
上的最小值。
（本小题满分12分）
数列
的前n项和为
，若
（1）求
（2）是否存在等比数列
满足
若存在，则求出数列的通项公式；若不存在，则说明理由。
（本小题满分10分）在锐角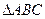
中，A、B、C三内角所对的边分别为a、b、c，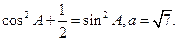
（1）若b=3，求c；
（2）求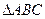的面积的最大值。