已知数列{an}中,a1=2,an=2- (n≥2,n∈N*).
(n≥2,n∈N*).
(1)设bn= ,n∈N*,求证:数列{bn}是等差数列;
,n∈N*,求证:数列{bn}是等差数列;
(2)设cn= (n∈N*),求数列{cn}的前n项和Sn.
(n∈N*),求数列{cn}的前n项和Sn.
已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.
(1)求该几何体的体积V;(2)求该几何体的侧面积S。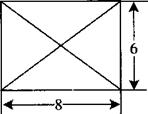
、(本小题满分13分).在正方体ABCD-A1B1C1D1中,M、N、P分别是CC1、B1C1、C1D1的中点.(温馨提示:该题要在答题卡上作图,否则扣分)。
(1) 求异面直线PN、AC所成角; (2) 求证:平面MNP∥平面A1BD.
定义在R上的函数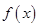 满足:对任意实数
满足:对任意实数 ,总有
,总有 ,且当
,且当 时,
时, .
.
(1)试求 的值;
的值;
(2)判断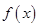 的单调性并证明你的结论;
的单调性并证明你的结论;
已知全集为U=R,A={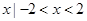 } ,B={
} ,B={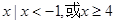 }
}
求:(1) (2)
(2)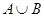 (3)
(3)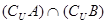
设数列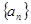 的前
的前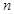 项和为
项和为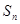 ,
,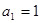 ,且对任意正整数
,且对任意正整数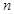 ,点
,点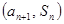 在直线
在直线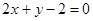 上.
上.
(Ⅰ) 求数列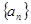 的通项公式;
的通项公式;
(Ⅱ)是否存在实数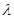 ,使得数列
,使得数列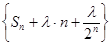 为等差数列?若存在,求出
为等差数列?若存在,求出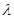 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.