随机抽取某中学甲、乙两班各10名同学，测量他们的身高(单位：cm)，获得身高数据的茎叶图如下图．
(1)根据茎叶图判断哪个班的平均身高较高；
(2)计算甲班的样本方差；
(3)现从乙班这10名同学中随机抽取两名身高不低于173 cm的同学，求身高为176 cm的同学被抽中的概率．
如图，已知四棱锥P－ABCD的底面为直角梯形，AB∥CD，∠DAB＝90°，PA⊥底面ABCD，且PA＝AD＝DC＝
AB＝1，M是PB的中点．
(1)求证：AM＝CM；
(2)若N是PC的中点，求证：DN∥平面AMC.
如图，四棱锥P－ABCD的底面ABCD是边长为2的菱形，∠BAD＝60°，已知PB＝PD＝2，PA＝
.
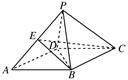
(1)证明：PC⊥BD；
(2)若E为PA的中点，求三棱锥P－BCE的体积．
如图，在三棱柱ABC－A1B1C1中，侧面AA1C1C⊥底面ABC，AA1＝A1C＝AC＝2，AB＝BC，AB⊥BC，O为AC中点．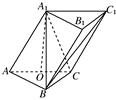
(1)证明：A1O⊥平面ABC；
(2)若E是线段A1B上一点，且满足VE－BCC1＝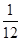
·VABC－A1B1C1，求A1E的长度．
已知点集L＝{(x，y)|y＝m·n}，其中m＝(2x－2b,1)，n＝(1,1＋2b)，点列Pn(an，bn)在点集L中，P1为L的轨迹与y轴的交点，已知数列{an}为等差数列，且公差为1，n∈N*.
(1)求数列{an}，{bn}的通项公式；
(2)求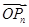
·OPn＋1的最小值；
(3)设cn＝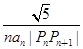
(n≥2)，求c2＋c3＋c4＋…＋cn的值．
已知数列{2n－1·an}的前n项和Sn＝1－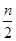
.
(1)求数列{an}的通项公式；
(2)设bn＝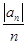
，求数列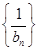
的前n项和．