我校为了了解高二级学生参加体育活动的情况，随机抽取了100名高二级学生进行调查．下面是根据调查结果绘制的学生日均参加体育活动时间的频率分布直方图：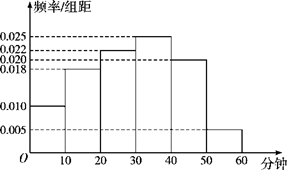
将日均参加体育活动时间不低于40分钟的学生称为参加体育活动的“积极分子”．根据已知条件完成下面的列联表，并据此资料，在犯错误的概率不超过5%的前提下，你是否认为参加体育活动的“积极分子”与性别有关？
| |
非积极分子 |
积极分子 |
合计 |
| 男 |
|
15 |
45 |
| 女 |
|
|
|
| 合计 |
|
|
|
已知全集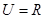
，集合
，
，
（1）求
、
；
（2）若集合
是集合A的子集，求实数k的取值范围.
（1）计算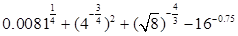
的值．
（2）计算
的值.
（本小题满分12分）如图，在三棱锥P- ABC中，PC⊥平面ABC，△ABC为正三角形，D，E，F分别是BC，PB，CA的中点．
（1）证明平面PBF⊥平面PAC；
（2）判断AE是否平行平面PFD？并说明理由；
（3）若PC =" AB" = 2，求三棱锥P - DEF的体积．
（本小题10分）如图，在四棱锥P－ABCD中，PA⊥底面ABCD，底面ABCD为正方形，PA＝AB＝2，M, N分别为PA, BC的中点．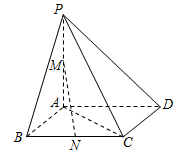
（Ⅰ）证明：MN∥平面PCD；
（Ⅱ）求MN与平面PAC所成角的正切值．
已知正方体
，求证：（１）
面
；（2 ）
⊥平面；