已知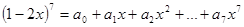
，求
（1）
的值。
（2）
的值。
（3）
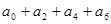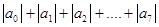的值。
已知函数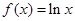
，
（1）求函数
的单调区间；
（2）当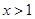
时，函数
恒成立，求实数
的取值范围；
（3）设正实数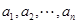
满足
．求证：
．
如图所示：已知过抛物线
的焦点F的直线
与抛物线相交于A，B两点。
（1）求证：以AF为直径的圆与x轴相切；
（2）设抛物线在A，B两点处的切线的交点为M，若点M的横坐标为2，求△ABM的外接圆方程；
（3）设过抛物线焦点F的直线与椭圆
的交点为C、D，是否存在直线使得
，若存在，求出直线的方程，若不存在，请说明理由。
数列{
}的前n项和为
，
，
．
（1）设
，证明：数列
是等比数列；
（2）求数列
的前
项和
；
（3）若
，
．求不超过
的最大整数的值。
在如图所示的几何体中，
是边长为2的正三角形，
平面ABC，平面
平面ABC，BD=CD，且
．
（1）若AE=2，求证：AC∥平面BDE；
（2）若二面角A—DE—B为60°．求AE的长。
的值．
的值.