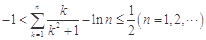某企业生产A，B两种产品，生产每吨产品所需的劳动力和煤、电耗如下表：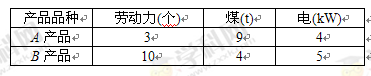
已知生产每吨A产品的利润是5万元，生产每吨B产品的利润是10万元，现因条件限制，该企业仅有劳动力300个，煤360 t，并且供电局只能供电200 kW，试问该企业生产A，B两种产品各多少吨，才能获得最大利润？
（本小题满分12分）在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且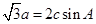
．
（1）求角C；
（2）若c＝
，且△ABC的面积为
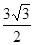
，求a＋b的值．
（本小题满分12分）某同学用五点法画函数
在某一个周期内的图像时，列表并填入了部分数据，如下表：
 |
0 |
 |
 |
 |
 |
 |
 |
 |
|||
 |
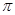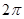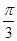0 |
5 |
-5 |
0 |
（1）请将上表数据补充完整，并直接写出函数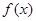
的解析式；
（2）若函数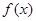的图像向左平移
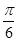个单位后对应的函数为
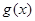，求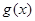的图像离原点最近的对称中心．
（本小题满分12分）已知向量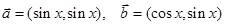
，若函数
（1）求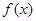
的最小正周期；
（2）若
，求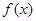的单调减区间．
（本小题满分10分）已知
，且
，
（1）求
的值；
（2）若
，
，求
的值．
（本小题满分12分）设函数
．
（1）若函数
在
处有极值，求函数的最大值；
（2）①是否存在实数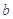
，使得关于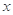
的不等式
在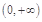
上恒成立？若存在，求出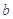的取值范围；若不存在，说明理由；
②证明：不等式