为了解甲、乙两厂产品的质量,从两厂生产的产品中分别随机抽取各9件样品,测量产品中某种元素的含量(单位:毫克).如图是测量数据的茎叶图,但是乙厂记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以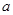 表示,规定:当产品中的此种元素含量不小于18毫克时,该产品为优等品.
表示,规定:当产品中的此种元素含量不小于18毫克时,该产品为优等品.
(Ⅰ)若甲、乙两厂产品中该种元素含量的平均值相同,求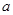 的值;
的值;
(Ⅱ)求乙厂该种元素含量的平均值超过甲厂平均值的概率;
(Ⅲ)当 时,利用简单随机抽样的方法,分别在甲、乙两厂该种元素含量超过
时,利用简单随机抽样的方法,分别在甲、乙两厂该种元素含量超过 (毫克)的数据中个抽取一个做代表,设抽取的两个数据中超过
(毫克)的数据中个抽取一个做代表,设抽取的两个数据中超过 (毫克)的个数为
(毫克)的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分13分)
等差数列 中,首项
中,首项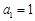 ,公差
,公差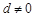 ,前n项和为
,前n项和为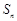 ,已知数列
,已知数列 成等比数列,其中
成等比数列,其中 ,
,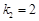 ,
, .
.
(Ⅰ)求数列 ,
,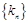 的通项公式;
的通项公式;
(Ⅱ)令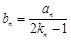 ,数列
,数列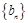 的前n项和为
的前n项和为 .若存在一个最小正整数M,使得当
.若存在一个最小正整数M,使得当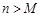 时,
时, (
( )恒成立,试求出这个最小正整数M的值.
)恒成立,试求出这个最小正整数M的值.
(本小题满分13分)
函数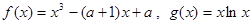 .
.
(Ⅰ)若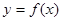 ,
,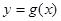 在
在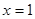 处的切线相互垂直,求这两个切线方程;
处的切线相互垂直,求这两个切线方程;
(Ⅱ)若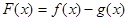 单调递增,求
单调递增,求 的范围.
的范围.
(本小题满分12分)
已知数列 的各项均为正数,且前
的各项均为正数,且前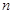 项之和
项之和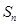 满足
满足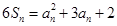 ,且
,且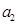 ,
,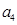 ,
,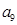 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)若数列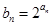 的前
的前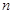 项和为
项和为 ,求
,求 .
.
(本小题满分13分)
如图,在六面体 中,平面
中,平面 ∥平面
∥平面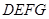 ,
, 平面
平面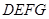 ,
, ,
,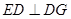 ,
, ∥
∥ ,且
,且 ,
,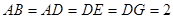 .
.
(1)求证:平面 平面
平面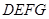 ;
;
(2)求证: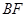 ∥平面
∥平面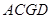 ;
;
(3)求三棱锥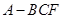 的体积.
的体积.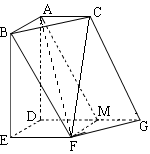
(本小题满分12分)
某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如下表所示. 已知在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16 .
| 第一批次 |
第二批次 |
第三批次 |
|
| 女教职工 |
196 |
x |
y |
| 男教职工 |
204 |
156 |
z |
(1)求 的值;
的值;
(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查, 问应在第三批次中抽取教职工多少名?
(3)已知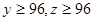 ,求第三批次中女教职工比男教职工多的概率.
,求第三批次中女教职工比男教职工多的概率.