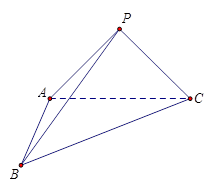
在三棱锥P-ABC中,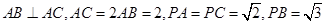 .
.
(1)求证:平面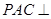 平面
平面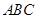 ;
;
(2)求BC与平面PAB所成角的正弦值.
((本小题满分14分)
已知函数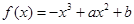
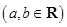 .
.
(1)求函数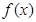 的单调递增区间;
的单调递增区间;
(2)若对任意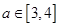 ,函数
,函数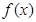 在
在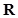 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围.
((本小题满分14分)
已知等差数列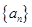 的公差
的公差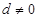 ,它的前
,它的前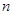 项和为
项和为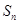 ,若
,若 ,且
,且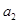 ,
,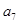 ,
,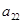 成等比数列.
成等比数列.
(1)求数列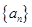 的通项公式;
的通项公式;
(2)设数列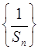 的前
的前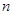 项和为
项和为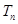 ,求证:
,求证: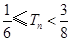 .
.
(本小题满分14分)
如图5所示,在三棱锥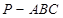 中,
中,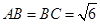 ,平面
,平面 平面
平面 ,
,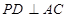 于点
于点 ,
, 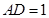 ,
,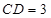 ,
,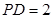 .
.
(1)求三棱锥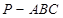 的体积;
的体积;
(2)证明△ 为直角三角形.
为直角三角形.
(本小题满分12分)某校从高一年级学生中随机抽取40名学生,将他们的期中考
试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段: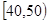 ,
,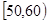 ,…,
,…,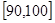 后得到如图4的频率分布直方图.
后得到如图4的频率分布直方图.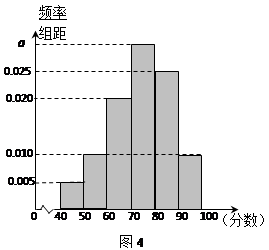
(1)求图中实数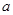 的值;
的值;
(2)若该校高一年级共有学生640人,试估计该校高一年级
期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在 与
与 两个分数段内的学
两个分数段内的学
生中随机选取两名学生,求这两名学生的数学成绩之差
的绝对值不大于10的概率.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
已知函数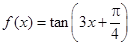 .
.
(1)求 的值;(2)若
的值;(2)若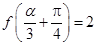 ,求
,求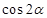 的值.
的值.