(本小题满分13分)某电视台的冲关电视节,要求参赛者从 道选题中一次性随机抽取
道选题中一次性随机抽取 道题,至少独立的正确回答
道题,至少独立的正确回答 道题,方可进入下一关.已知
道题,方可进入下一关.已知 道备选题中参赛者小福有
道备选题中参赛者小福有 道题能正确回答,
道题能正确回答, 道题不能正确回答;参赛者小州每题正确回答的概率都是
道题不能正确回答;参赛者小州每题正确回答的概率都是 ,且每题正确回答与否互不影响.
,且每题正确回答与否互不影响.
(Ⅰ)分别求小福、小州两人正确回答试题数的分布列,并计算其数学期望;
(Ⅱ)请分析比较小福、小州两人谁进入下一关的可能性大.
(本小题满分13分)如图,在四棱锥PABCD中,侧面PAD⊥底面ABCD,侧棱
 ,
, ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,O为AD中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的大小;
所成角的大小;
已知函数
(Ⅰ)求 的单调增区间;
的单调增区间;
(Ⅱ)若 ,求
,求 的最大值和最小值.
的最大值和最小值.
若数列 的各项均为正数,
的各项均为正数, ,
, 为常数,且
为常数,且 .
.
(1)求 的值;
的值;
(2)证明:数列 为等差数列;
为等差数列;
(3)若 ,对任意给定的k∈N*,是否存在p,r∈N*(k<p<r)使
,对任意给定的k∈N*,是否存在p,r∈N*(k<p<r)使 ,
, ,
, 成等差数列?若存在,用k分别表示一组p和r;若不存在,请说明理由.
成等差数列?若存在,用k分别表示一组p和r;若不存在,请说明理由.
函数 .
.
(1)若 ,求曲线
,求曲线 在
在 的切线方程;
的切线方程;
(2)若函数 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(3)设点 ,
,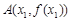 ,
, 满足
满足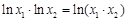
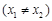 ,判断是否存在实数
,判断是否存在实数 ,使得
,使得 为直角?说明理由.
为直角?说明理由.