某网站针对“2014年法定节假日调休安排”展开的问卷调查,提出了A、B、C三种放假方案,调查结果如下:
| |
支持A方案 |
支持B方案 |
支持C方案 |
| 35岁以下 |
200 |
400 |
800 |
| 35岁以上(含35岁) |
100 |
100 |
400 |
(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从“支持A方案”的人中抽取了6人,求n的值;
(2)在“支持B方案”的人中,用分层抽样的方法抽取5人看作一个总体,从这5人中任意选取2人,求恰好有1人在35岁以上(含35岁)的概率.
如图,在五面体,ABCDF中,点O是矩形ABCD的对角线的交点,面ABF是等边三角形,棱EF=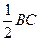 .
.
(1)证明EO∥平面ABF;
(2)问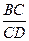 为何值时,有OF⊥ABE,试证明你的结论.
为何值时,有OF⊥ABE,试证明你的结论.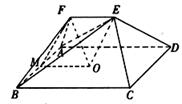
如图,已知AB⊥平面ACD,DE//AB,△ACD是正三角形,AD=DE=2AB,且F
是CD的中点。
(I)求证:AF//平面BCE;
(II)求证:平面BCE⊥平面CDE;
(III)求平面BCE与平面ACD所成锐二面角的大小。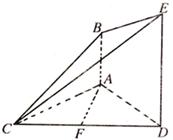
如图,在四棱锥 中,底面 是矩形,已知 .

(1)证明:
平面
;
(2)求异面直线
与
所成的角的大小;
(3)求二面角
的大小.
如图,在四棱锥P—ABCD中,PA⊥底面ABCD,∠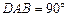 , AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.
, AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.
(Ⅰ)证明:CD⊥平面BEF;
(Ⅱ)设 ,
,
求k的值.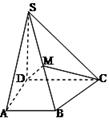
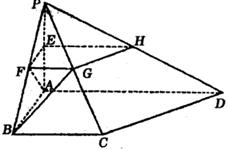
四棱锥P—ABCD中,PA⊥面ABCD,PA=AB=BC=2,E为PA中点,过E作平行于底面的面EFGH分别与另外三条侧棱交于F,G,H,已知底面ABCD为直角梯形,AD//BC,AB⊥AD,∠BCD=135°
(1)求异面直线AF,BG所成的角的大小;
(2)设面APB与面CPD所成的锐二面角的大小为θ,求cosθ.