直三棱柱
的底面为等腰直角三角形，
，
，
分别是
的中点。求异面直线
和
所成角的大小。
已知集合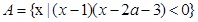
，函数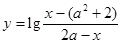
的定义域为集合B.
(1)若
，求集合
;
(2)已知
且“
”是“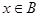
”的必要不充分条件，求实数a的取值范围.
若等边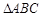
的边长为
，平面内一点
满足
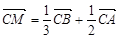，求
．
已知函数f(x)=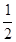
-ax(a∈R,e为自然对数的底数).
(1)讨论函数f(x)的单调性；
(2)若a=1，函数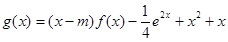
在区间（0，+
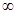）上为增函数，求整数m的最大值.
已知函数
和
的定义域都是[2，4].
若
,求
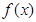的最小值；
若
在其定义域上有解，求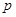
的取值范围；
若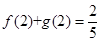
，求证
.
为了了解青少年视力情况，某市从高考体检中随机抽取16名学生的视力进行调查，经医生用对数视力表检查得到每个学生的视力状况的茎叶图（以小数点前的一位数字为茎，小数点后的一位数字为叶）如下：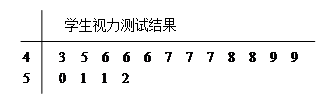
（1）若视力测试结果不低丁5．0，则称为“好视力”，求校医从这16人中随机选取3人，至多有1人是“好视力”的概率；
（2）以这16人的样本数据来估计该市所有参加高考学生的的总体数据，若从该市参加高考的学生中任选3人，记
表示抽到“好视力”学生的人数，求的分布列及数学期望．