已知直线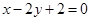 经过椭圆
经过椭圆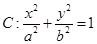 (
(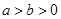 )的左顶点
)的左顶点 和
和
上顶点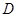 .椭圆
.椭圆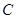 的右顶点为
的右顶点为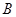 ,点
,点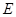 是椭圆
是椭圆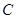 上位于
上位于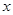 轴上方的动点,直线
轴上方的动点,直线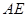 、
、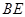 与直线
与直线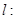
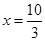 分别交于
分别交于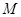 、
、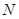 两点.
两点.
(Ⅰ)求椭圆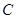 的标准方程;
的标准方程;
(Ⅱ)求线段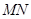 长度的最小值;
长度的最小值;
(Ⅲ)当线段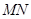 的长度最小时,椭圆
的长度最小时,椭圆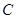 上是否存在这样的点
上是否存在这样的点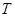 ,使得
,使得 的面积为
的面积为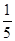 ?若存在,确定点
?若存在,确定点 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.
已知函数 (
( ),
), (
( ).
).
(Ⅰ)若函数 在
在 处的切线方程为
处的切线方程为 ,求实数
,求实数 与
与 的值;
的值;
(Ⅱ)求 的单调减区间;
的单调减区间;
(Ⅲ)当 时,若对任意的
时,若对任意的 ,存在
,存在 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.
如图,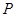 为某湖中观光岛屿,
为某湖中观光岛屿,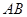 是沿湖岸南北方向道路,
是沿湖岸南北方向道路,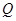 为停车场,
为停车场,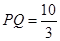
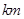 ,某旅游团浏览完岛屿后,乘游船回停车场
,某旅游团浏览完岛屿后,乘游船回停车场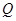 ,已知游船以
,已知游船以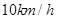 的速度沿方位角
的速度沿方位角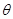 的
的
方向行驶,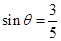 .游船离开观光岛屿
.游船离开观光岛屿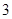 分钟后,因事耽搁没有来得及登上游船的游客甲,为了及时
分钟后,因事耽搁没有来得及登上游船的游客甲,为了及时
赶到停车地点 与旅游团会合,立即决定租用小艇先到达湖岸南北大道
与旅游团会合,立即决定租用小艇先到达湖岸南北大道 处,然后乘景区电动出租车到
处,然后乘景区电动出租车到
停车场 处(假设游客甲到达湖滨大道后幸运地一点未耽搁便乘上了电动出租车).游客甲乘小艇行驶的
处(假设游客甲到达湖滨大道后幸运地一点未耽搁便乘上了电动出租车).游客甲乘小艇行驶的
方位角是 ,电动出租车的速度为
,电动出租车的速度为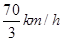 .
.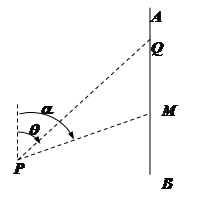
(Ⅰ)设 ,问小艇的速度为多少
,问小艇的速度为多少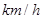 时,游客甲才能与游船同时到达点
时,游客甲才能与游船同时到达点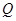 ;
;
(Ⅱ)设小艇速度为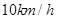 ,请你替该游客设计小艇行驶的方位角
,请你替该游客设计小艇行驶的方位角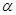 ,当角
,当角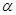 的余弦值是多少时,游客甲能按计划以最短时间到达
的余弦值是多少时,游客甲能按计划以最短时间到达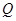 .
.
如图,矩形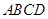 中,
中,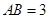 ,
,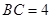 ,
,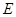 、
、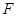 分别在线段
分别在线段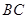 和
和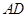 上,
上,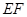 ∥
∥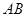 ,将矩形
,将矩形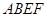 沿
沿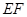 折起,记折起后的矩形为
折起,记折起后的矩形为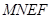 ,且平面
,且平面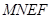
 平面
平面 .
.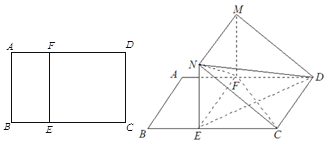
(Ⅰ)求证: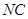 ∥平面
∥平面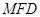 ;
;
(Ⅱ)求四面体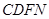 体积的最大值.
体积的最大值.
如图所示,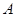 、
、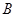 分别是单位圆与
分别是单位圆与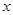 轴、
轴、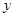 轴正半轴的交点,点
轴正半轴的交点,点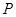 在单位圆上,
在单位圆上,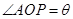 (
( ),点
),点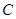 坐标为
坐标为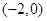 ,平行四边形
,平行四边形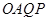 的面积为
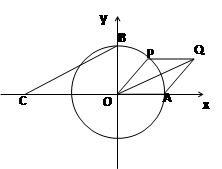
的面积为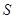 .
.
(Ⅰ)求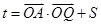 的最大值;
的最大值;
(Ⅱ)若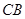 ∥
∥ ,求
,求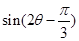 .
.