为了了解青少年视力情况，某市从高考体检中随机抽取16名学生的视力进行调查，经医生用对数视力表检查得到每个学生的视力状况的茎叶图（以小数点前的一位数字为茎，小数点后的一位数字为叶）如下：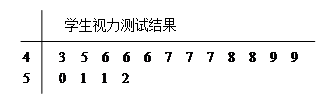
（1）若视力测试结果不低丁5．0，则称为“好视力”，求校医从这16人中随机选取3人，至多有1人是“好视力”的概率；
（2）以这16人的样本数据来估计该市所有参加高考学生的的总体数据，若从该市参加高考的学生中任选3人，记
表示抽到“好视力”学生的人数，求的分布列及数学期望．
给定两个命题,P：对任意实数x都有
x2+x+1＞0恒成立；Q：关于x的方程x2-x+=0有实数根.如果P∨Q为真命题，P∧Q为假命题，求实数的取值范围．
已知函数
的图象在点
（ｅ为自然对数的底数）处取得极值－１.
（1）求实数
的值；
（2）若不等式
对任意
恒成立，求
的取值范围．
已知椭圆Ｃ：
的左、右焦点和短轴的一个端点构成边长为４的正三角形．
（1）求椭圆Ｃ的方程；
（2）过右焦点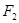
的直线
与椭圆Ｃ相交于Ａ、Ｂ两点，若
，求直线的方程．
某公司欲建连成片的网球场数座，用２８８万元购买土地２００００平方米，每座球场的建筑面积为１０００平方米，球场每平方米的平均建筑费用与所建的球场数有关，当该球场建ｎ座时，每平方米的平均建筑费用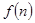
表示，且
（其中
），又知建５座球场时，每平方米的平均建筑费用为４００元．
（1）为了使该球场每平方米的综合费用最省（综合费用是建筑费用与购地费用之和），公司应建几座网球场？
（2）若球场每平方米的综合费用不超过８２０元，最多建几座网球场？
在
中，
分别是角Ａ，Ｂ，Ｃ的对边，且满足
．
（1）求角Ｂ的大小；
（2）若最大边的边长为
，且
，求最小边长．