如图,AB为⊙O的直径,弦CD与AB相交于E,DE=EC,过点B的切线与AD的延长线交于F,过E作EG⊥BC于G,延长GE交AD于H。
(1)求证:AH=HD;
(2)若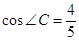 ,DF=9,求⊙O的半径。
,DF=9,求⊙O的半径。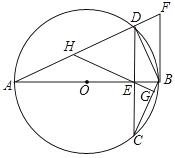
已知:如图,等边△ABC中,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE=∠BDF,点M在线段DF上,∠ABE=∠DBM.
(1)猜想:线段AE、MD之间有怎样的数量关系,并加以证明;
(2)在(1)的条件下延长BM到P,使MP=BM,连接CP,若AB=7 ,AE=
,AE= ,
,
求tan∠BCP的值.
已知:关于 的一元二次方程
的一元二次方程

(1) 若方程有两个不相等的实数根,求 的取值范围;
的取值范围;
(2)求证:无论 为何值,方程总有一个固定的根;
为何值,方程总有一个固定的根;
(3)若 为整数,且方程的两个根均为正整数,求
为整数,且方程的两个根均为正整数,求 的值.
的值.
如图,将正方形沿图中虚线(其 )剪成① ② ③ ④ 四块图形,用这四块图形恰好能拼成一个矩形(非正方形).
)剪成① ② ③ ④ 四块图形,用这四块图形恰好能拼成一个矩形(非正方形).
(1)画出拼成的矩形的简图;
(2)求 的值.
的值.
学校为了学生的身体健康,每天开展体育活动一小时,开设排球、篮球、羽毛球、体操课.学生可根据自己的爱好任选其中一项,老师根据学生报名情况进行了统计,并绘制 了右边尚未完成的扇形统计图和频数分布直方图,请你结合图中的信息,解答下列问题:
了右边尚未完成的扇形统计图和频数分布直方图,请你结合图中的信息,解答下列问题:
(1)该校学生报名总人数有多少人?
(2)从表中可知选羽毛球的学生有多少人?选排球和篮球的人数分别占报名总人数的百分之几?
(3)将两个统计图补充完整.
已知:如图, 是
是 的直径,
的直径, 切
切 于
于 ,
, 交
交 于
于 ,
, 为
为 边的中点,连结
边的中点,连结 .
.
(1)  是
是 的切线;
的切线;
(2) 若 ,
,  的半径为5, 求
的半径为5, 求 的长.
的长.